题目内容
给定一个n项的实数列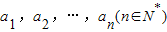 ,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”
,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”(Ⅰ)对数列:1,2,4,8,分别写出经变换T1(2),T2(3),T3(4)后得到的数列;
(Ⅱ)对数列:1,3,5,7,给出一个“k次归零变换”,其中k≤4;
(Ⅲ)证明:对任意n项数列,都存在“n次归零变换”.
【答案】分析:(Ⅰ)根据新定义,可计算经变换T1(2),T2(3),T3(4)后得到的数列;
(Ⅱ)根据新定义,计算经变换T1(4);T2(2);T3(1),或T1(2);T2(2);T3(2);T4(1),可得结论;
(Ⅲ)记经过Tk(ck)变换后,数列为 .取
.取 ,
, ,继续做类似的变换,取
,继续做类似的变换,取 ,(k≤n-1),经Tk(ck)后,得到数列的前k+1项相等,再取
,(k≤n-1),经Tk(ck)后,得到数列的前k+1项相等,再取 ,经Tn(cn)后,即可得到结论.
,经Tn(cn)后,即可得到结论.
解答:(Ⅰ)解:T1(2):1,0,2,6;T2(3):2,3,1,3;T3(4):2,1,3,1.…(3分)
(Ⅱ)解:方法1:T1(4):3,1,1,3;T2(2):1,1,1,1;T3(1):0,0,0,0.
方法2:T1(2):1,1,3,5;T2(2):1,1,1,3;T3(2):1,1,1,1;T4(1):0,0,0,0.
…(6分)
(Ⅲ)证明:记经过Tk(ck)变换后,数列为 .
.
取 ,则
,则 ,即经T1(c1)后,前两项相等;
,即经T1(c1)后,前两项相等;
取 ,则
,则 ,即经T2(c2)后,前3项相等;
,即经T2(c2)后,前3项相等;
继续做类似的变换,取 ,(k≤n-1),经Tk(ck)后,得到数列的前k+1项相等.特别地,当k=n-1时,各项都相等,最后,取
,(k≤n-1),经Tk(ck)后,得到数列的前k+1项相等.特别地,当k=n-1时,各项都相等,最后,取 ,经Tn(cn)后,数列各项均为0.所以必存在n次“归零变换”. …(13分)
,经Tn(cn)后,数列各项均为0.所以必存在n次“归零变换”. …(13分)
点评:本题考查新定义,考查学生分析解决问题的能力,考查学生的探究能力,难度较大.
(Ⅱ)根据新定义,计算经变换T1(4);T2(2);T3(1),或T1(2);T2(2);T3(2);T4(1),可得结论;
(Ⅲ)记经过Tk(ck)变换后,数列为
 .取
.取 ,
, ,继续做类似的变换,取
,继续做类似的变换,取 ,(k≤n-1),经Tk(ck)后,得到数列的前k+1项相等,再取
,(k≤n-1),经Tk(ck)后,得到数列的前k+1项相等,再取 ,经Tn(cn)后,即可得到结论.
,经Tn(cn)后,即可得到结论.解答:(Ⅰ)解:T1(2):1,0,2,6;T2(3):2,3,1,3;T3(4):2,1,3,1.…(3分)
(Ⅱ)解:方法1:T1(4):3,1,1,3;T2(2):1,1,1,1;T3(1):0,0,0,0.
方法2:T1(2):1,1,3,5;T2(2):1,1,1,3;T3(2):1,1,1,1;T4(1):0,0,0,0.
…(6分)
(Ⅲ)证明:记经过Tk(ck)变换后,数列为
 .
.取
 ,则
,则 ,即经T1(c1)后,前两项相等;
,即经T1(c1)后,前两项相等;取
 ,则
,则 ,即经T2(c2)后,前3项相等;
,即经T2(c2)后,前3项相等;继续做类似的变换,取
 ,(k≤n-1),经Tk(ck)后,得到数列的前k+1项相等.特别地,当k=n-1时,各项都相等,最后,取
,(k≤n-1),经Tk(ck)后,得到数列的前k+1项相等.特别地,当k=n-1时,各项都相等,最后,取 ,经Tn(cn)后,数列各项均为0.所以必存在n次“归零变换”. …(13分)
,经Tn(cn)后,数列各项均为0.所以必存在n次“归零变换”. …(13分)点评:本题考查新定义,考查学生分析解决问题的能力,考查学生的探究能力,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
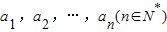 ,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”.
,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”.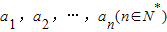 ,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”.
,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”.