题目内容
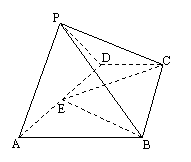
如图，四棱锥P-ABCD中，侧面PAD⊥底面ABCD，底面ABCD是梯形，且AB∥CD，AB=2CD，BE⊥EC，E为AD的中点，PA=PD.
（Ⅰ）求证：BE⊥PC；
（Ⅱ）在棱PA上是否存在一点M，使得DM∥平面PBC.若存在，找出这个点；若不存在，说明理由.
 |
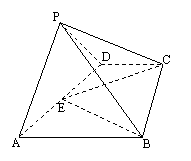
（Ⅰ）证明：连接PE
 |
∵PA=PD ∴PE⊥AD
又 平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD
∴PE⊥平面ABCD ∴PE⊥BE
又BE⊥EC, BE∩EC=E
∴BE⊥平面PEC 又PC
平面PEC
∴BE⊥PC ……6分
（Ⅱ）分别取PA和PB的中点M、N，连接MD,MN,NC
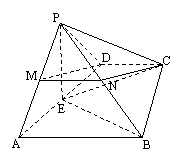
则MN∥AB,且2MN=AB
又AB∥CD，AB=2CD ∴MN∥CD，MN=CD
∴四边形MNCD是平行四边形
∴MD∥NC
又 MD
平面PBC，NC平面PBC
∴DM∥平面PBC
∴当点M是棱PA的中点时，有DM∥平面PBC ……12分
练习册系列答案
相关题目
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，
如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD=2，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°，M为AP的中点．
如图，四棱锥P-ABCD的底面ABCD是矩形，AB=2，
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，且PA=AB=1，
如图，四棱锥P-ABCD，PA⊥平面ABCD，ABCD是直角梯形，DA⊥AB，CB⊥AB，PA=2AD=BC=2，AB=