题目内容
已知定义在（﹣1，1）上的函数f（x），满足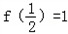
，并且
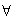x，y∈（﹣1，1）都有
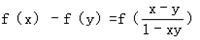成立，对于数列{xn}，有
．
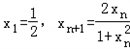（Ⅰ）求f（0），并证明f（x）为奇函数；
（Ⅱ）求数列{f（xn）}的通项公式；
（Ⅲ）对于(II）中的数列{f（xn）}，
证明：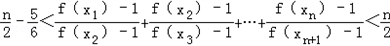
（n∈N*）．
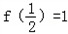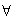，并且x，y∈（﹣1，1）都有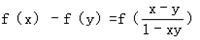成立，对于数列{xn}，有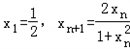．（Ⅰ）求f（0），并证明f（x）为奇函数；
（Ⅱ）求数列{f（xn）}的通项公式；
（Ⅲ）对于(II）中的数列{f（xn）}，
证明：
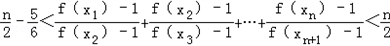（n∈N*）．解：（1）当x=y=0时，f（0）=0，再令x=0
得f（0）﹣f（y）=f（﹣y）
即f（y）+f（﹣y）=0
∴f（x）在（﹣1，1）上为奇函数．
（2）由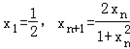
易知0＜xn＜1
∵f（xn）﹣f（﹣xn）=f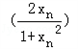
且f（x）且f（x）在（﹣1，1）上为奇函数
∴f（xn+1）=2f（xn），f（x1）=1
∴f（xn）是以1为首项，2为公比的等比数列
∴f（xn）=2n﹣1
（3）
=
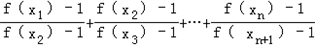
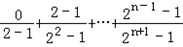
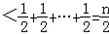
得f（0）﹣f（y）=f（﹣y）
即f（y）+f（﹣y）=0
∴f（x）在（﹣1，1）上为奇函数．
（2）由
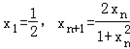易知0＜xn＜1∵f（xn）﹣f（﹣xn）=f
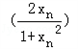
且f（x）且f（x）在（﹣1，1）上为奇函数
∴f（xn+1）=2f（xn），f（x1）=1
∴f（xn）是以1为首项，2为公比的等比数列
∴f（xn）=2n﹣1
（3）
=
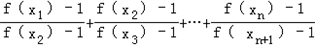
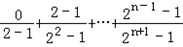
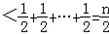
练习册系列答案
相关题目
．
为奇函数．．
为奇函数．．
为奇函数．．