题目内容
【题目】【2017北京西城区5月模拟】已知函数
，其中
.
（Ⅰ）求函数
的零点个数；
（Ⅱ）证明：
是函数
存在最小值的充分而不必要条件.
【答案】（I）详见解析；（II）详见解析.
【解析】
（Ⅰ）由
，
得
令
，得
，或
.
所以当
时，函数
有且只有一个零点：
；当
时，函数
有两个相异的零点：
，
.
（Ⅱ）①当
时，
恒成立，此时函数
在
上单调递减，
所以，函数
无极值.
②当
时，
，
的变化情况如下表：
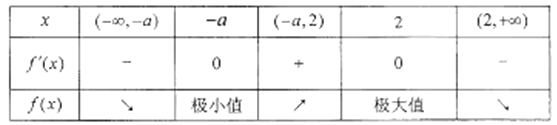
所以，
时，
的极小值为
.
又
时，
，
所以，当
时，
恒成立.
所以，
为
的最小值.
故
是函数
存在最小值的充分条件.
③当
时，
，
的变化情况如下表：
因为当
时，
，
又
，
所以，当
时，函数
也存在最小值.
所以，
不是函数
存在最小值的必要条件.
综上，
是函数
存在最小值的充分而不必要条件.
点睛;本题注意考查了导数与函数的极值、最值的关系，属于中档题.涉及的考点有：用导数研究函数的极值、最值，充分不必要条件的判断，根的存在及个数判断.考查了学生分析问题和转化的能力以及分类讨论思想.
练习册系列答案
相关题目
