题目内容
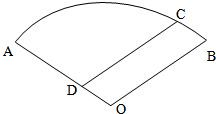 如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,小区的两个出入口设置在点A及点C处,且小区里有一条平行于BO的小路CD,已知某人从C沿CD走到D用了10分钟,从D沿DA走到A用了6分钟,若此人步行的速度为每分钟50米,求该扇形的半径OA的长(精确到1米)
如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,小区的两个出入口设置在点A及点C处,且小区里有一条平行于BO的小路CD,已知某人从C沿CD走到D用了10分钟,从D沿DA走到A用了6分钟,若此人步行的速度为每分钟50米,求该扇形的半径OA的长(精确到1米)
分析:连接OC,由CD∥OB知∠CDO=60°,可由余弦定理得到OC的长度.
解答: 解:[法一]设该扇形的半径为r米,连接CO.
解:[法一]设该扇形的半径为r米,连接CO.
由题意,得CD=500(米),DA=300(米),∠CDO=60°
在△CDO中,CD2+OD2-2CD•OD•cos60°=OC2
即,5002+(r-300)2-2×500×(r-300)×
=r2
解得r=
≈445(米)
答:该扇形的半径OA的长约为445米.
 [法二]连接AC,作OH⊥AC,交AC于H,
[法二]连接AC,作OH⊥AC,交AC于H,
由题意,得CD=500(米),AD=300(米),∠CDA=120°
在△CDO中,AC2=CD2+AD2-2•CD•AD•cos120°=5002+3002+2×500×300×
=7002.
∴AC=700(米).(6分)cos∠CAD=
=
.
在直角△HAO中,AH=350(米),cos∠HAO=
,
∴OA=
=
≈445(米).
答:该扇形的半径OA的长约为445米.
 解:[法一]设该扇形的半径为r米,连接CO.
解:[法一]设该扇形的半径为r米,连接CO.由题意,得CD=500(米),DA=300(米),∠CDO=60°
在△CDO中,CD2+OD2-2CD•OD•cos60°=OC2
即,5002+(r-300)2-2×500×(r-300)×
| 1 |
| 2 |
解得r=
| 4900 |
| 11 |
答:该扇形的半径OA的长约为445米.
 [法二]连接AC,作OH⊥AC,交AC于H,
[法二]连接AC,作OH⊥AC,交AC于H,由题意,得CD=500(米),AD=300(米),∠CDA=120°
在△CDO中,AC2=CD2+AD2-2•CD•AD•cos120°=5002+3002+2×500×300×
| 1 |
| 2 |
∴AC=700(米).(6分)cos∠CAD=
| AC2+AD2-CD2 |
| 2•AC•AD |
| 11 |
| 14 |
在直角△HAO中,AH=350(米),cos∠HAO=
| 11 |
| 14 |
∴OA=
| AH |
| cos∠HAO |
| 4900 |
| 11 |
答:该扇形的半径OA的长约为445米.
点评:本题主要考查用余弦定理求三角形边长.

练习册系列答案
相关题目
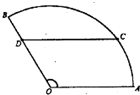 如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径为
如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径为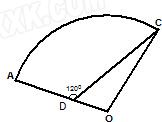 如图,某住宅小区的平面图呈扇形AOC.小区的两个出入口设置在点A及点C处,小区里有两条笔直的小路AD,DC,且拐弯处的转角为120°.已知某人从C沿CD走到D用了10分钟,从D沿DA走到A用了6分钟.若此人步行的速度为每分钟50米,则该扇形的半径OA的长为
如图,某住宅小区的平面图呈扇形AOC.小区的两个出入口设置在点A及点C处,小区里有两条笔直的小路AD,DC,且拐弯处的转角为120°.已知某人从C沿CD走到D用了10分钟,从D沿DA走到A用了6分钟.若此人步行的速度为每分钟50米,则该扇形的半径OA的长为 如图,某住宅小区的平面图呈扇形AOC.小区的两个出入口设置在点A及点C处,小区里有两条笔直的小路AD,CD,且拐弯处的转角为120°.已知某人从C沿CD走到D用了10分钟,从D沿DA走到A用了6分钟.若此人步行的速度为每分钟50米,求该扇形的半径OA的长(精确到1米).
如图,某住宅小区的平面图呈扇形AOC.小区的两个出入口设置在点A及点C处,小区里有两条笔直的小路AD,CD,且拐弯处的转角为120°.已知某人从C沿CD走到D用了10分钟,从D沿DA走到A用了6分钟.若此人步行的速度为每分钟50米,求该扇形的半径OA的长(精确到1米).