题目内容
已知
是等比数列
的前n项的和，
成等差数列.
（1）求等比数列的公比
；
（2）判断
是否成等差数列？若成等差数列，请给出证明；若不成等差数列，
请说明理由.
（1）由题意有：
………………………………1分
所以 
因为
所以 
即
………………………………4分
解得 
所以 
………………7分
(2) ① 当
时
因为
所以时
不成等差数列； ………………………………10分
② 当
时，知
所以
.
所以 
所以时，成等差数列. ………………………13分
综上：当时不成等差数列；当时，成等差数列. 14分
练习册系列答案
相关题目
相切，则α的值为( )A.1 B. 2 C.-1 D.-2
y)10的展开式中x6y4项的系数是（ ）
840 
－840 
210 
－210
等于( )
B.2 C. 
D.4
如图，正三棱柱
的底面边长为
，当正视图的视线方向垂直于平面
时，正视图的面积为
，则此时左视图的面积为________.
B．
C．
D． 
（
，
，
）的部分图象如图所示，则
（ ）
A.
B.
D.
对应的点的坐标在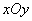 
中，曲线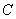
的参数方程为
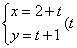为参数），以该直角坐标系的原点为极点，
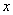轴的正半轴为极轴的极坐标系下，曲线
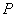的方程为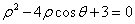
.
.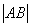