题目内容
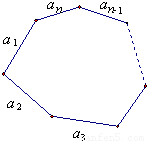
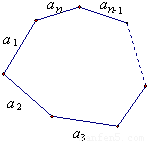
对一个边长互不相等的凸n(n≥3)边形的边染色,每条边可以染红、黄、蓝三种颜色中的一种,但是不允许相邻的边有相同的颜色.问:共有多少种不同的染色方法?分析:设n边形的不同的染色方法有pn种,由题意得p3=
=6,根据当n≥4时,pn=3×2n-1-pn-1,数列{Pn-2n}为公比为-1的等比数列,这样可求得Pn-2n的通项公式,从而求得Pn.
| A | 3 3 |
解答:解:设n边形的不同的染色方法有pn种.易知三角形的染色方法p3=
=6.
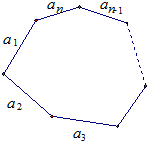
当n≥4时,首先,对于边a1,有3种不同的染法,由于边a2的颜色与边a1的颜色不同,
∴对边a2有2种不同的染法,类似地,对边a3,…,边an-1均有2种染法.对于边an,用与边an-1不同的2种颜色染色,
但是,这样也包括了它与边a1颜色相同的情况,
而边a1与边an颜色相同的不同染色方法数就是凸n-1边形的不同染色方法数的种数pn-1,
∴pn=3×2n-1-pn-1,pn-2n=-(pn-1-2n-1).数列{Pn-2n}为公比为-1的等比数列,
∴pn-2n=(-1)n-3(p3-23)=(-1)n-2•2,
∴pn=2n+(-1)n•2,n≥3.
综上所述,不同的染色方法数为pn=2n+(-1)n•2.
| A | 3 3 |

当n≥4时,首先,对于边a1,有3种不同的染法,由于边a2的颜色与边a1的颜色不同,
∴对边a2有2种不同的染法,类似地,对边a3,…,边an-1均有2种染法.对于边an,用与边an-1不同的2种颜色染色,
但是,这样也包括了它与边a1颜色相同的情况,
而边a1与边an颜色相同的不同染色方法数就是凸n-1边形的不同染色方法数的种数pn-1,
∴pn=3×2n-1-pn-1,pn-2n=-(pn-1-2n-1).数列{Pn-2n}为公比为-1的等比数列,
∴pn-2n=(-1)n-3(p3-23)=(-1)n-2•2,
∴pn=2n+(-1)n•2,n≥3.
综上所述,不同的染色方法数为pn=2n+(-1)n•2.
点评:解答本题的关键是利用n边形的染色方法数与n-1边形的染色方法数的关系,构造等比数列求Pn.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
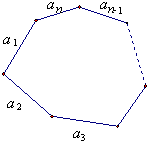 对一个边长互不相等的凸n(n≥3)边形的边染色,每条边可以染红、黄、蓝三种颜色中的一种,但是不允许相邻的边有相同的颜色.所有不同的染色方法记为P(n)
对一个边长互不相等的凸n(n≥3)边形的边染色,每条边可以染红、黄、蓝三种颜色中的一种,但是不允许相邻的边有相同的颜色.所有不同的染色方法记为P(n)