题目内容
已知函数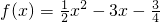 .定义函数f(x)与实数m的一种符号运算为m?f(x)=f(x)•[f(x+m)-f(x)].
.定义函数f(x)与实数m的一种符号运算为m?f(x)=f(x)•[f(x+m)-f(x)].
(1)求使函数值f(x)大于0的x的取值范围;
(2)若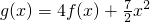 ,求g(x)在区间[0,4]上的最大值与最小值;
,求g(x)在区间[0,4]上的最大值与最小值;
(3)是否存在一个数列{an},使得其前n项和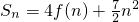 .若存在,求出其通项;若不存在,请说明理由.
.若存在,求出其通项;若不存在,请说明理由.
解:(1)由f(x)>0,得 ,
,
即2x2-12x-3>0,解得 或
或 .
.
所以,x的取值范围为  .
.
(2)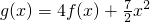 =
= =
= =
= =
= .
.
对g(x)求导,得g'(x)=6x2-21x+9=3(x-3)(2x-1).
令g'(x)=0,解得 或x=3.
或x=3.
当x变化时,g'(x)、g(x)的变化情况如下表:
| x | 0 |  |  |  | 3 | (3,4) | 4 |
| g'(x) | + | 0 | - | 0 | + | ||
| g(x) | 3 | ↗ |  | ↘ |  | ↗ | -1 |
所以,g(x)在区间[0,4]上的最大值为 ,最小值为
,最小值为 .
.
(3)存在.
由(2)得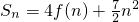 =
=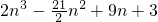 .
.
当n≥2时,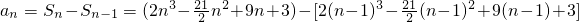 =
=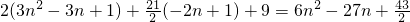
当n=1时,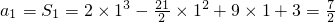 .
.
所以, .
.
分析:(1)函数值f(x)大于0的x的取值范围通过解不等式函数
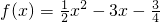 >0求出即可.
>0求出即可.(2)根据题设中的定义,将g(x)计算化简并整理,应得出g(x)=
 ,再利用导数求出g(x)在区间[0,4]上的最大值与最小值
,再利用导数求出g(x)在区间[0,4]上的最大值与最小值(3)由(2)得
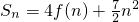 =
=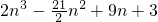 ,转化为利用数列中an与 Sn关系求数列通项.
,转化为利用数列中an与 Sn关系求数列通项.点评:本题考查了一元二次不等式解法、利用导数研究最大(小)值.以及利用数列中an与 Sn关系求数列通项.考查转化、变形、计算能力.

练习册系列答案
相关题目
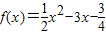 .定义函数f(x)与实数m的一种符号运算为m?f(x)=f(x)•[f(x+m)-f(x)].
.定义函数f(x)与实数m的一种符号运算为m?f(x)=f(x)•[f(x+m)-f(x)]. ,求g(x)在区间[0,4]上的最大值与最小值.
,求g(x)在区间[0,4]上的最大值与最小值.