题目内容
是否存在两个锐角α,β满足.
(1)α+2β=
;
(2)tan
•tanβ=2-
同时成立,若存在,求出α,β的值;若不存在,说明理由.
(1)α+2β=
| 2π |
| 3 |
(2)tan
| α |
| 2 |
| 3 |
由(1)得
+β=
,∴
=tan(
+β)=
,得tan
+tanβ=3-
,又因为tan
•tanβ=2-
∴将tan
=
代入得tanβ=1;将tanβ=
得tan
=1(∵0<
<
,∴tan
≠1,舍去),
∴tanβ=1
∴
为所求满足条件的两个锐角.
| α |
| 2 |
| π |
| 3 |
| 3 |
| α |
| 2 |
tan
| ||
1-tan
|
| α |
| 2 |
| 3 |
| α |
| 2 |
| 3 |
∴将tan
| α |
| 2 |
2-
| ||
| tanβ |
2-
| ||
tan
|
| α |
| 2 |
| α |
| 2 |
| π |
| 4 |
| α |
| 2 |
∴tanβ=1
∴
|

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 ;
; 同时成立,若存在,求出α,β的值;若不存在,说明理由.
同时成立,若存在,求出α,β的值;若不存在,说明理由.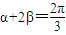 ;
; 同时成立,若存在,求出α,β的值;若不存在,说明理由.
同时成立,若存在,求出α,β的值;若不存在,说明理由.