Question

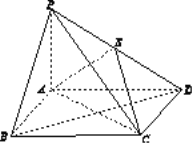
【题目】（本题满分12分）如图13，四棱锥P ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．

(1)证明：PB∥平面AEC；

(2)设AP＝1，AD＝，三棱锥P ABD的体积V＝，求A到平面PBC的距离．

Answer 1

【答案】（1）略（2）

【解析】试题分析：证明线面平有两种思路，一是寻求线线平行，二是寻求面面平行；已知三棱锥的体积求点到平面的距离，可借助面面垂直的性质定理根据三棱锥的体积求出长，由于平面PAB，可以得出平面平面，可借助面面垂直的性质定理做出点，垂足为，可得平面，即的长为点到平面的距离，再求出，这是一种传统方法.

试题解析：

(1)证明：设BD与AC的交点为O，连接EO.

因为ABCD为矩形，所以O为BD的中点．

又E为PD的中点，所以EO∥PB.

EO平面AEC，PB平面AEC，

所以PB∥平面AEC.

(2)V＝××PA×AB×AD＝AB，由V＝，可得AB＝.

作AH⊥PB交PB于点H.

由题设知BC⊥平面PAB，所以BC⊥AH，因为PB∩BC＝B，所以AH⊥平面PBC.

又AH＝＝，

所以点A到平面PBC的距离为