题目内容
已知数列
的前
项和
满足：
，且
（1）求
（2）猜想的通项公式，并用数学归纳法证明.
解：（1）
，所以
，
，又 ∵
，所以
.
， 所以 
,
所以
.
（2）猜想
．
证明： 
当
时，由（1）知成立．
假设
时，
成立
．
所以
所以当
时猜想也成立．
综上可知，猜想对一切
都成立．
练习册系列答案
名校课堂系列答案
相关题目
个单位长度，再把所得图象上所有点的横坐标缩短到原来的
倍(纵坐标不变)，得到的图象所表示的函数是( )
是函数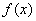
的极值点，求曲线
.
.
的值为
C．2 D．4
，则三棱锥A-BCD的外接球的大圆面积为
B. 
C. 
D. 
B．
C.40 D.80
的共轭复数为 ( )
, B. 
, C. 
D.