题目内容
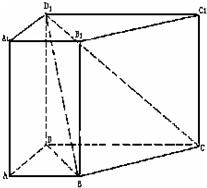
已知直四棱柱ABCD-A1B1C1D1中，AA1=2，底面ABCD是直角梯形，∠A是直角，AB∥CD，AB=4，AD=2，DC=1，求异面直线BC1与DC所成角的大小。（结果用反三角函数值表示）
| 解：由题意AB∥CD， ∴  是异面直线BC1与DC所成的角，连结AC1与AC， 在Rt△ADC中，可得  ，又在Rt△ACC1中，可得AC1=3， 在梯形ABCD中，过C作CH∥AD交AB于H， 得  ，∴  ，又在  中，可得 ，在  ，∴  ， ∴异面直线BC1与DC所成角的大小为  。 |
 |
练习册系列答案
阅读快车系列答案
相关题目
已知直四棱柱ABCD-A1B1C1D1中，AB∥CD，AB=AD=1，DD1=CD=2，AB⊥AD．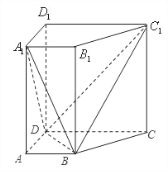
如图所示，已知直四棱柱ABCD-A1B1C1D1中，AD⊥DCAB∥DC，且满足
如图，已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形，∠BAD=60°，AA1=6，P是棱AA1的中点．求：
已知直四棱柱ABCD-A1B1C1D1的底面是菱形，F为棱BB1的中点，M为线段AC1的中点．
（2010•宝山区模拟）已知直四棱柱ABCD-A1B1C1D1体积为32，且底面四边形ABCD为直角梯形，其中上底BC=2，下底AD=6，腰AB=2，且BC⊥AB．