题目内容
如图，四棱锥P—ABCD的底面是边长为a的正方形，侧棱PA⊥底面ABCD，侧面PBC内有BE⊥PC于E，且BE=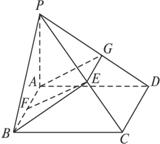
a，试在AB上找一点F，使EF∥平面PAD.
解：在面PCD内作EG⊥PD于G，连结AG.
∵PA⊥平面ABCD，CD⊥AD，
∴CD⊥PD.
∴CD∥EG.
又AB∥CD，
∴EG∥AB.
若有EF∥平面PAD，则EF∥AG，
∴四边形AFEG为平行四边形，得EG=AF.
∵CE=
=a,△PBC为直角三角形，
∴BC2=CE·CP
CP=
a,
=
=
=
=
.
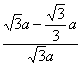故当AF∶FB=2∶1时，EF∥平面PAD.
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，
如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD=2，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°，M为AP的中点．
如图，四棱锥P-ABCD的底面ABCD是矩形，AB=2，
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，且PA=AB=1，
如图，四棱锥P-ABCD，PA⊥平面ABCD，ABCD是直角梯形，DA⊥AB，CB⊥AB，PA=2AD=BC=2，AB=