题目内容
(Ⅰ)设![]() 证明:
证明:![]() ,
,
(Ⅱ)![]() ,证明
,证明![]() .
.
证明(1)要证原不等式只要证x2y+xy2+1≤x+y+x2y2,下面用做差法证明:
(x+y+x2y2)-(x2y+xy2+1)=(xy-1)(x-1)(y-1)>0
所以原不等式得证
(2)∵logab·logbc=logac∴原不等式化为
logab+logbc+![]() ≤
≤![]() +
+![]() +logac
+logac
令logab=x≥1,logbc=y≥1,∴由(1)可知不等式成立。

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目

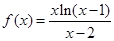 .
.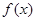 的单调性;
的单调性;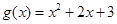 ,证明:对任意
,证明:对任意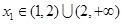 ,总存在
,总存在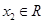 ,使得
,使得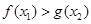 .
. 的前
的前 项和为
项和为 ,已知
,已知
 证明数列
证明数列 是等比数列;
是等比数列; 与
与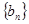 中,
中,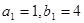 ,数列
,数列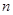 项和
项和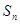 满足
满足 ,
,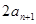 为
为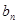 与
与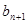 的等比中项,
的等比中项, .
.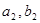 的值;
的值;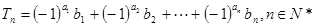 .证明
.证明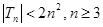 .
. 的前n项积为
的前n项积为 ;数列
;数列 的前n项和为
的前n项和为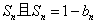 .
.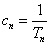 .①证明数列
.①证明数列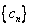 成等差数列;②求证数列
成等差数列;②求证数列 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.