题目内容
已知函数f(x)=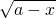 +
+ (a∈N*),对定义域内任意x1,x2,满足|f(x1)-f(x2)|<1,则正整数a的取值个数是________.
(a∈N*),对定义域内任意x1,x2,满足|f(x1)-f(x2)|<1,则正整数a的取值个数是________.
5
分析:对定义域内任意x1,x2,满足|f(x1)-f(x2)|<1,即表明f(x)的最大值与最小值的差小于1.(也就是值域区间的长度小于1),求其最大最小值即可.
解答:∵a-x≥0,x≥0,∴0≤x≤a,∴定义域为[0,a]
对定义域内任意x1,x2,满足|f(x1)-f(x2)|<1,即表明f(x)的最大值与最小值的差小于1.(也就是值域区间的长度小于1),求其最大最小值即可
∵f(x)=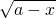 +
+ ≥0
≥0
∴[f(x)]2=a+2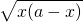 ≥a,当x=0或a时,f(x)取最小值
≥a,当x=0或a时,f(x)取最小值
又x(a-x)≤[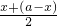 ]2=
]2= ,当x=a-x即x=
,当x=a-x即x= 时取等号
时取等号
即[f(x)]2≤a+a=2a,f(x)≤ ,当x=
,当x= 时取最大值
时取最大值
∴( -1)
-1) <1
<1
∴ <
<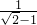 =1+
=1+
∴a<3+2
∵a∈N*,
∴a=1、2、3、4、5
∴正整数a的取值个数是5个.
故答案为:5
点评:本题考查恒成立问题,考查函数的最值,解题的关键是转化为值域区间的长度小于1.
分析:对定义域内任意x1,x2,满足|f(x1)-f(x2)|<1,即表明f(x)的最大值与最小值的差小于1.(也就是值域区间的长度小于1),求其最大最小值即可.
解答:∵a-x≥0,x≥0,∴0≤x≤a,∴定义域为[0,a]
对定义域内任意x1,x2,满足|f(x1)-f(x2)|<1,即表明f(x)的最大值与最小值的差小于1.(也就是值域区间的长度小于1),求其最大最小值即可
∵f(x)=
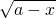 +
+ ≥0
≥0∴[f(x)]2=a+2
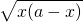 ≥a,当x=0或a时,f(x)取最小值
≥a,当x=0或a时,f(x)取最小值
又x(a-x)≤[
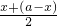 ]2=
]2= ,当x=a-x即x=
,当x=a-x即x= 时取等号
时取等号即[f(x)]2≤a+a=2a,f(x)≤
 ,当x=
,当x= 时取最大值
时取最大值
∴(
 -1)
-1) <1
<1∴
 <
<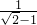 =1+
=1+
∴a<3+2

∵a∈N*,
∴a=1、2、3、4、5
∴正整数a的取值个数是5个.
故答案为:5
点评:本题考查恒成立问题,考查函数的最值,解题的关键是转化为值域区间的长度小于1.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|