Question

（本小题满分12分）

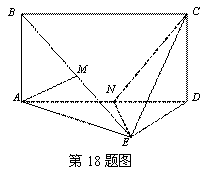已知矩形与正三角形所在的平面互相垂直， 、分别为棱、的中点，,，

(1)证明：直线平面；

(2)求二面角的大小．

Answer 1

（1）证明：方法一：

取EC的中点F，连接FM，FN，

则，，，  ………………………2分

所以且，所以四边形为平行四边形，

所以，                            …………………………………4分

因为平面，平面，

所以直线平面；                   …………………………………6分

（2）解：由题设知面面，，

又，∴面，作于，则，作，连接，由三垂线定理可知，

∴就是二面角的平面角，   …………………………………9分

在正中，可得，在中，可得，故在中，，                      …………………………………11分

所以二面角的大小为       …………………………………12分

      

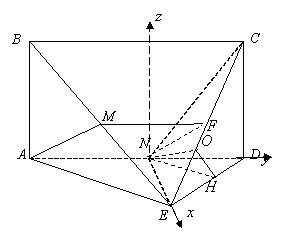
方法二：如图以N为坐标原点建立空间右手

直角坐标系,所以 

 …1分

（1）取EC的中点F ，所以，                   

设平面的一个法向量为，因为，

所以，；所以，  ……………3分

因为，，所以   ………………………5分

因为平面，所以直线平面     ………………………7分

（2）设平面的一个法向量为，因为，

所以，；所以……………9分

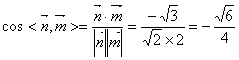         ………………………………11分

因为二面角的大小为锐角,

所以二面角的大小为     ………………………………12分