题目内容
己知函数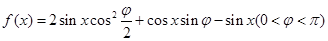 ,在
,在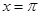 处取最小值.
处取最小值.
(1)求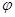 的值;
的值;
(2)在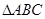 中,
中,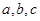 分别是
分别是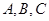 的对边,已知
的对边,已知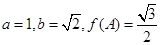 ,求角
,求角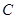 .
.
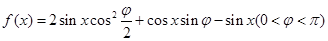 ,在
,在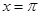 处取最小值.
处取最小值.(1)求
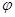 的值;
的值;(2)在
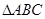 中,
中,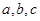 分别是
分别是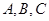 的对边,已知
的对边,已知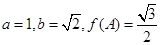 ,求角
,求角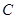 .
.(1)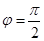 ;(2)
;(2)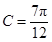 或
或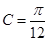 .
.
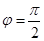 ;(2)
;(2)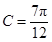 或
或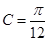 .
.试题分析:(1)先将函数解析式化为形如
 ,这时要用倍角公式、降幂公式、两角和的正弦公式,得到
,这时要用倍角公式、降幂公式、两角和的正弦公式,得到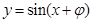 ,再利用
,再利用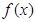 在
在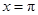 处取得最小值得关于
处取得最小值得关于 的关系式
的关系式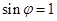 ,结合限制条件
,结合限制条件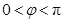 ,解出
,解出 ;(2)解三角形问题,主要利用正余弦定理,本题可由
;(2)解三角形问题,主要利用正余弦定理,本题可由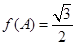 ,解出角
,解出角 ,由正弦定理得
,由正弦定理得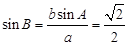 ,解出角
,解出角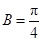 或
或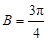 ,再由三角形内角和为
,再由三角形内角和为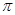 ,解出
,解出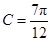 或
或 ,本题求解角
,本题求解角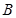 时,需注意解的个数,因为正弦函数在
时,需注意解的个数,因为正弦函数在 上有增有减.,所以有两个解.
上有增有减.,所以有两个解.试题解析:(1)
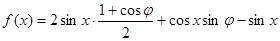
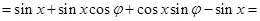
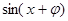 3分
3分因为
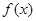 在
在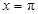 处取得最小值,所以
处取得最小值,所以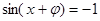
故
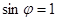 ,又
,又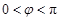
所以
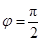 6分
6分(2)由(1)知

因为
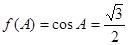 ,且
,且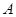 为
为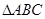 的内角
的内角所以
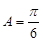 ,由正弦定理得
,由正弦定理得 ,所以
,所以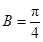 或
或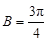 9分
9分当
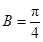 时,
时,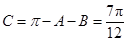
当
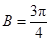 时,
时,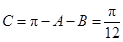
综上,
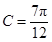 或
或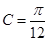 12分.
12分.
练习册系列答案
相关题目
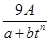 ,其中
,其中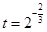 ,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍. 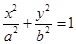 (a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q).
(a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q). 的最小值为
的最小值为 ,求椭圆的方程.
,求椭圆的方程.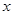 ,有
,有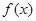 为奇函数,
为奇函数,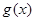 为偶函数,且
为偶函数,且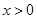 时,
时,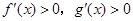 ,则
,则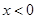 时( )
时( )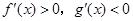
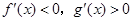
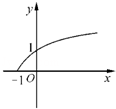
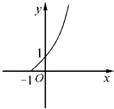
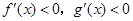 导数
导数 ﹣1的图象大致是( )
﹣1的图象大致是( )
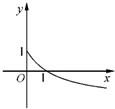
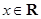 ,
,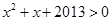 ”的否定是“任意
”的否定是“任意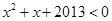 ”
” 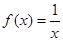 在其定义域上是减函数
在其定义域上是减函数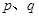 ,若“
,若“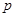 且
且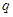 ”是真命题,则
”是真命题,则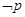 是假命题
是假命题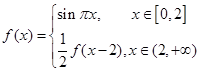 ,有下列4个命题:
,有下列4个命题: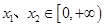 ,都有
,都有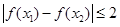 恒成立;
恒成立;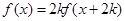
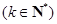 ,对于一切
,对于一切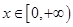 恒成立;
恒成立;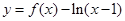 有3个零点;
有3个零点;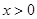 ,不等式
,不等式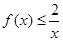 恒成立.
恒成立.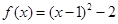 的递增区间是___________________ .
的递增区间是___________________ .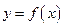 的图象与
的图象与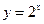 的图象关于直线
的图象关于直线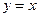 对称,则函数
对称,则函数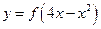 的递增区间是_________.
的递增区间是_________.