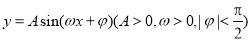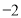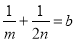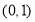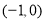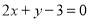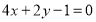题目内容
在平面直角坐标系中，给定
，点
为
的中点，点
满足
，点
满足
.
（1）求
与
的值；
（2）若
三点坐标分别为
，求
点坐标.
（1）
；（2）
点的坐标为
.
【解析】
试题分析：先引入平面向量的基底，如
，然后将
分别用基底表示，最后得到
，而另一方面
，再根据平面向量的基本定理得到方程组
，求解方程组即可；（2）先确定
的坐标，设
，再结合
，得到
，从而得到
，求解即可得到
点的坐标.
试题解析：（1）设
则
2分
，
，
故 4分
而
由平面向量基本定理得，解得 6分
（2）
、
、
，由于
为
中点，
9分
设，又由（1）知
所以
可得，解之得
所以点的坐标为 12分.
考点：1.平面向量的线性运算；2.平面向量的基本定理；3.平面向量的坐标运算.
练习册系列答案
阅读快车系列答案
相关题目
