题目内容
设函数f(x)=![]() x3+x2+(m2-1)x,(x∈R,)其中m>0
x3+x2+(m2-1)x,(x∈R,)其中m>0
(1)当m=1时,曲线y=f(x)在点(1,f(1))处的切线方程
(2)求函数的单调区间与极值;
(3)已知函数f(x)有三个互不相同的零点0,x1,x2,且x1<x2.若对任意的x∈[x1,x2],f(x)>f(1)恒成立,求m的取值范围.
答案:
解析:
解析:
|
解:设函数 解析:当 (2)解析 因为
f(x)在(-∞,1-m)和(1+m,+∞)内减函数,在(1-m,1+m)内增函数. 函数 函数 (3)解析:由题设, 所以方程 因为 若 若 则 综上,m的取值范围是 |

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 x3-
x3- x2+a x.
x2+a x.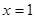 处的切线方程为12x+y-1=0.
处的切线方程为12x+y-1=0. 上的最大值和最小值.
上的最大值和最小值.