题目内容
设函数 ,若f(x)+f′(x)为偶函数,则φ=________.
,若f(x)+f′(x)为偶函数,则φ=________.
-
分析:通过化简可得f(x)+f′(x)=2sin( x+φ+
x+φ+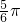 ),由f(x)+f′(x)为偶函数,知当x=0时f(x)+f′(x)取得最值,由此可得φ+
),由f(x)+f′(x)为偶函数,知当x=0时f(x)+f′(x)取得最值,由此可得φ+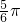 =kπ
=kπ ,k∈Z,根据φ的范围即可解得φ值.
,k∈Z,根据φ的范围即可解得φ值.
解答:f(x)+f′(x)=cos( x+φ)-
x+φ)- sin(
sin( x+φ)=2sin(
x+φ)=2sin( x+φ+
x+φ+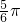 ),
),
因为f(x)+f′(x)为偶函数,
所以当x=0时2sin( x+φ+
x+φ+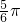 )=±2,则φ+
)=±2,则φ+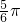 =kπ
=kπ ,k∈Z,
,k∈Z,
所以φ=kπ- ,k∈Z,
,k∈Z,
又-π<φ<0,
所以φ=- .
.
故答案为:- .
.
点评:本题考查导数的运算、函数的奇偶性及三角恒等变换,考查学生对问题的理解解决能力,属中档题.

分析:通过化简可得f(x)+f′(x)=2sin(
 x+φ+
x+φ+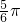 ),由f(x)+f′(x)为偶函数,知当x=0时f(x)+f′(x)取得最值,由此可得φ+
),由f(x)+f′(x)为偶函数,知当x=0时f(x)+f′(x)取得最值,由此可得φ+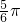 =kπ
=kπ ,k∈Z,根据φ的范围即可解得φ值.
,k∈Z,根据φ的范围即可解得φ值.解答:f(x)+f′(x)=cos(
 x+φ)-
x+φ)- sin(
sin( x+φ)=2sin(
x+φ)=2sin( x+φ+
x+φ+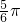 ),
),因为f(x)+f′(x)为偶函数,
所以当x=0时2sin(
 x+φ+
x+φ+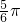 )=±2,则φ+
)=±2,则φ+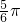 =kπ
=kπ ,k∈Z,
,k∈Z,所以φ=kπ-
 ,k∈Z,
,k∈Z,又-π<φ<0,
所以φ=-
 .
.故答案为:-
 .
.点评:本题考查导数的运算、函数的奇偶性及三角恒等变换,考查学生对问题的理解解决能力,属中档题.

练习册系列答案
相关题目
 ,若f(x)=10,则x= .
,若f(x)=10,则x= .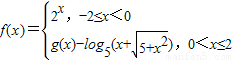 ,若f(x)是奇函数,则当x∈(0,2]时,g(x)的最大值是( )
,若f(x)是奇函数,则当x∈(0,2]时,g(x)的最大值是( )
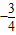

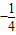
 ,(ω∈R,ω>0),设函数
,(ω∈R,ω>0),设函数 ,若f(x)的最小正周期为
,若f(x)的最小正周期为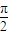 .
.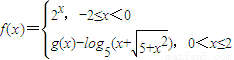 ,若f(x)是奇函数,则当x∈(0,2]时,g(x)的最大值是( )
,若f(x)是奇函数,则当x∈(0,2]时,g(x)的最大值是( )
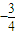

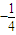
 ,
, ,其中ω为常数,且ω>0.
,其中ω为常数,且ω>0. ∥
∥ ,求tanx的值;
,求tanx的值; ,若f(x)的最小正周期为π,求f(x)在
,若f(x)的最小正周期为π,求f(x)在 时的值域.
时的值域.