题目内容
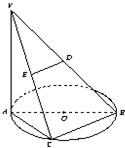 18、如图,AB是圆O的的直径,点C是弧AB的中点,D,E分别是VB,VC的中点,VA⊥平面ABC.
18、如图,AB是圆O的的直径,点C是弧AB的中点,D,E分别是VB,VC的中点,VA⊥平面ABC.(Ⅰ)求异面直线DE与AB所成的角;
(Ⅱ)证明DE⊥平面VAC.
分析:(1)将ED平移到BC,易证∠ABC是异面直线DE与AB所成的角,而△ABC是以∠ACB为直角的等腰直角三角形,则∠ABC为45°
(2)欲证DE⊥平面VAC,而BC∥DE,可先证BC⊥平面VAC,根据线面垂直的判定定理可知只需证BC⊥VA,BC⊥AC即可.
(2)欲证DE⊥平面VAC,而BC∥DE,可先证BC⊥平面VAC,根据线面垂直的判定定理可知只需证BC⊥VA,BC⊥AC即可.
解答: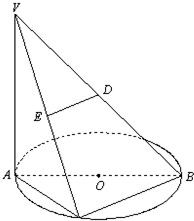 解(Ⅰ)因为D,E分别是VB,VC的中点,
解(Ⅰ)因为D,E分别是VB,VC的中点,
所以BC∥DE,因此∠ABC是异面直线DE
与AB所成的角.(3分)
又因为AB是圆O的的直径,点C是弧AB的
中点,所以△ABC是以∠ACB为直角的等腰直角三角形.于是∠ABC=45°.
故异面直线DE与AB所成的角为45°.(6分)
(Ⅱ)因为VA⊥平面ABC,BC?平面ABC,所以BC⊥VA.(8分)
由(Ⅰ)知,BC⊥AC,所以BC⊥平面VAC.(10分)
又由(Ⅰ)知,BC∥DE,故DE⊥平面VAC.(12分)
 解(Ⅰ)因为D,E分别是VB,VC的中点,
解(Ⅰ)因为D,E分别是VB,VC的中点,所以BC∥DE,因此∠ABC是异面直线DE
与AB所成的角.(3分)
又因为AB是圆O的的直径,点C是弧AB的
中点,所以△ABC是以∠ACB为直角的等腰直角三角形.于是∠ABC=45°.
故异面直线DE与AB所成的角为45°.(6分)
(Ⅱ)因为VA⊥平面ABC,BC?平面ABC,所以BC⊥VA.(8分)
由(Ⅰ)知,BC⊥AC,所以BC⊥平面VAC.(10分)
又由(Ⅰ)知,BC∥DE,故DE⊥平面VAC.(12分)
点评:本题主要考查线线,线面关系的基础知识,以及直线与平面垂直的判定,同时考查空间想象能力和推理运算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
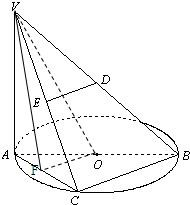 16、如图,AB是圆O的的直径,点C是弧AB的中点,D、E、F分别是VB,VC,AC的中点,VA⊥平面ABC.
16、如图,AB是圆O的的直径,点C是弧AB的中点,D、E、F分别是VB,VC,AC的中点,VA⊥平面ABC. (2013•湖北)如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
(2013•湖北)如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点. (2011•通州区一模)如图.AB是圆O的弦,弦PQ平行于过点B的切线BT,AP的延长线交切线BT于点M,PA=3PM=6.∠PAB=30°.则∠QAB的度数为
(2011•通州区一模)如图.AB是圆O的弦,弦PQ平行于过点B的切线BT,AP的延长线交切线BT于点M,PA=3PM=6.∠PAB=30°.则∠QAB的度数为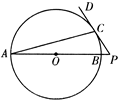 (1)如图,AB是圆O的直径,P在AB的延长线上,PD切圆O于点C.已知圆O半径为y=x-1(1≤x≤2),OP=2,则PC=
(1)如图,AB是圆O的直径,P在AB的延长线上,PD切圆O于点C.已知圆O半径为y=x-1(1≤x≤2),OP=2,则PC=