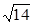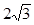题目内容
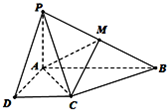
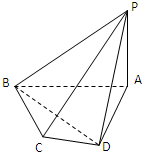
在如图所示的四棱锥P-ABCD中,已知PA⊥平面ABCD,AB∥DC,∠DAB=90°,PA=AD=DC=1,AB=2,M为PB的中点.
(1)求证:平面PAC⊥平面PBC;
(2)求二面角A-PB-C的平面角的正切值.
(1)求证:平面PAC⊥平面PBC;
(2)求二面角A-PB-C的平面角的正切值.

(1)取AB的中点H,连接CH,则CH⊥AB
∵PA⊥平面ABCD,∴PA⊥BC,∵AB∥DC,∠DAB=90°,
∴AC=BC=
.
又AC2+BC2=2+2=AB2,∴AC⊥BC,
∴BC⊥平面PAC,∵BC?平面PBC,
∴平面PAC⊥平面PBC….(7分)
(2)取AB的中点H,连接CH,则由题意得
CH⊥AB,又PA⊥平面ABCD,所以PA⊥CH,
则CH⊥平面PAB.所以CH⊥PB,过H作HG⊥PB于G,连接CG,则PB⊥平面CGH,
所以CG⊥PB,则∠CGH为二面角A-PB-C的平面角…(10分)
∵PA=1,∴CH=1,AB=2,PB=
=
则GH=BHsin∠PBA=BH•
=
,
∴tan∠CGH=
=
…(13分)
故二面角A-PB-C的平面角的正切值为
…(14分)

∵PA⊥平面ABCD,∴PA⊥BC,∵AB∥DC,∠DAB=90°,
∴AC=BC=
| 2 |
又AC2+BC2=2+2=AB2,∴AC⊥BC,
∴BC⊥平面PAC,∵BC?平面PBC,
∴平面PAC⊥平面PBC….(7分)
(2)取AB的中点H,连接CH,则由题意得
CH⊥AB,又PA⊥平面ABCD,所以PA⊥CH,
则CH⊥平面PAB.所以CH⊥PB,过H作HG⊥PB于G,连接CG,则PB⊥平面CGH,
所以CG⊥PB,则∠CGH为二面角A-PB-C的平面角…(10分)
∵PA=1,∴CH=1,AB=2,PB=
| PA2+AB2 |
| 5 |
则GH=BHsin∠PBA=BH•
| PA |
| AB |
| 1 | ||
|
∴tan∠CGH=
| CH |
| GH |
| 5 |
故二面角A-PB-C的平面角的正切值为
| 5 |


练习册系列答案
相关题目
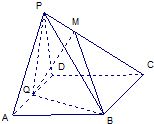


 内的射影,则OB等于( )
内的射影,则OB等于( )