题目内容

△ABC中若有sinC=
sinA+sinB
cosA+cosB
，则△ABC的形状一定是（　　）
分析：利用积化和差将等式变形，转化方向是变成简单的三角方程求角的值，通过角的值来确定△ABC的形状．
解答：证明：∵在△ABC中，sinC=
sinA+sinB
cosA+cosB

∴sin（A+B）=
2sin
A+B
2
×cos
A-B
2
2cos
A+B
2
cos
A-B
2

∴2sin
A+B
2
cos
A+B
2
=
sin
A+B
2
cos
A+B
2

∴2cos2
A+B
2
-1=0
∴cos（A+B）=0
∴A+B=
π
2
，即C=
π
2
，
∴△ABC是直角三角形．
故选B．
点评：考查利用三角恒等变换的公式进行灵活变形的能力，用来训练答题者掌握相关公式的熟练程度及选择变形方向的能力．
练习册系列答案
相关题目
给出下列命题：
①在△ABC中，若A＜B，则sinA＜sinB；
②将函数y=sin(2图象向右平移
π
3
个单位，得到函数y=sin2x的图象；
③在△ABC中，若AB=2，AC=3，∠ABC=60°，则△ABC必为锐角三角形；
④在同一坐标系中，函数y=sinx的图象和函数y=
x
2
的图象有三个公共点．
其中真命题是
 
．（填出所有正确命题的序号）
下列正确的有（　　）
①若f（x）=sinax+cosax，则y=f（x）既不是奇函数也不是偶函数；
②若α是三角形的内角，则y=sinα+cosα有最大值
2
，最小值不存在；
③函数y=sin|x|是最小正周期为π的周期函数；
④在△ABC中，若sinA＞sinB，则A＞B．
已知下列命题四个命题：
①若f（x）是定义在[-1，1]上的偶函数，且在[-1，0）上是增函数，θ∈(
π
4
，
π
2
)，则f（sinθ）＞f（cosθ）；
②在△ABC中，A＞B是cosA＜cosB的充要条件；
③设函数f（x）=x2+2（-2≤x＜0），其反函数为f-1（x），则f-1（3）=-1或1．
④在△ABC中，角A、B、C所对的边分别为a、b、c，已知b2+c2=a2+bc，则A=
π
3
．
其中真命题的个数有（　　）
（2012•福建模拟）阅读下面材料：
根据两角和与差的正弦公式，有sin（α+β）=sinαcosβ+cosαsinβ------①
sin（α-β）=sinαcosβ-cosαsinβ------②
由①+②得sin（α+β）+sin（α-β）=2sinαcosβ------③
令α+β=A，α-β=B有α=
A+B
2
，β=
A-B
2

代入③得 sinA+sinB=2sin
A+B
2
cos
A-B
2
．
（Ⅰ）类比上述推证方法，根据两角和与差的余弦公式，证明：cosA-cosB=-2sin
A+B
2
sin
A-B
2
；
（Ⅱ）若△ABC的三个内角A，B，C满足cos2A-cos2B=2sin2C，试判断△ABC的形状．
（提示：如果需要，也可以直接利用阅读材料及（Ⅰ）中的结论）

∆ABC中，有下列命题① ② ③则∆ABC是等腰三角形④若sin(A-)=，则角A=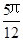。其中正确的结论是

A ②③④        B ①③④         C ②④            D ②③

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网