题目内容
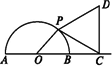
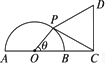
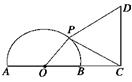
如图所示,已知半圆的直径AB=2,点C在AB的延长线上,BC=1,点P为半圆上的一个动点,以DC为边作等边△PCD,且点D与圆心O分别在PC的两侧,判断四边形OPDC的面积有无最大值.若有,求出最大值;若没有,说明理由.
思路分析:要判断四边形OPDC的面积有无最大值,这首先需要建立一个面积函数看这一个函数有无最大值,本题中建立目标函数的关键是选谁作为自变量,如果注意到动点P在半圆上运动与∠POB大小变化之间的联系,自然引入∠POB=θ作为自变量建立函数关系.四边形OPDC可以分成△OPC与等边△PDC,S△OPC可用![]() ·OP·OC·sinθ表示,而等边△PDC的面积关键在于边长的求解,而边长PC可以在△POC中利用余弦定理表示,至于面积最值的获得,则通过三角函数知识解决.
·OP·OC·sinθ表示,而等边△PDC的面积关键在于边长的求解,而边长PC可以在△POC中利用余弦定理表示,至于面积最值的获得,则通过三角函数知识解决.
解:设∠POB=θ,四边形面积为y,则在△POC中,由余弦定理,得
PC2=OP2?+OC2-2OP·OCcosθ=5-4cosθ,
∴y=S△OPC+S△PCD=![]() ×1×2sinθ+
×1×2sinθ+![]() (5-4cosθ)
(5-4cosθ)
=2sin(θ-![]() )+
)+![]() .
.
∴当θ-![]() =
=![]() ,即θ=
,即θ=![]() 时,ymax=2+
时,ymax=2+![]() .
.
方法归纳 本题中余弦定理为表示△PCD的面积,从而为表示四边形OPDC面积提供了可能,可见正、余弦定理不仅是解三角形的依据,一般地也是分析几何量之间关系的重要公式,要认识到这两个定理的重要性.另外,在求三角函数最值时,涉及到两角和正弦公式sin(α+β)=sinαcosβ+cosαsinβ的构造及逆用,应予以重视.

练习册系列答案
相关题目
 的延长线上,BC=1,点P为半圆上的一个动点,以
的延长线上,BC=1,点P为半圆上的一个动点,以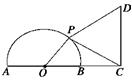 的延长线上,BC=1,点P为半圆上的一个动点,以
的延长线上,BC=1,点P为半圆上的一个动点,以