题目内容
若盒中装有同一型号的灯泡共 只,其中有
只,其中有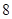 只合格品,
只合格品, 只次品。
只次品。
(1) 某工人师傅有放回地连续从该盒中取灯泡 次,每次取一只灯泡,求
次,每次取一只灯泡,求 次取到次品的概率;
次取到次品的概率;
(2) 某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求成功更换会议室的已坏灯泡所用灯泡只数 的分布列和数学期望.
的分布列和数学期望.
(1)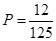 ;(2)分布列详见解析,
;(2)分布列详见解析,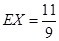 .
.
解析试题分析:本题主要考查古典概型及其概率计算公式、独立重复试验、离散型随机变量的分布列与数学期望等基础知识,考查运用概率知识解决简单实际问题的能力.第一问,先根据古典概型概率公式得到取得次品的概率,再根据独立重复试验的公式求3次中2次取到次品的概率;第二问,先写出灯泡只数 的所有可能情况,列出每一种情况的概率,根据上述概率的值直接列出分布列的表格,再用期望的计算公式计算.
的所有可能情况,列出每一种情况的概率,根据上述概率的值直接列出分布列的表格,再用期望的计算公式计算.
试题解析:设一次取次品记为事件 ,由古典概型概率公式得:
,由古典概型概率公式得: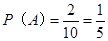 2 分
2 分
有放回连续取3次,其中2次取得次品记为事件 ,由独立重复试验得:
,由独立重复试验得: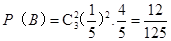 4分
4分
(2)依据知 的可能取值为1.2.3 5分
的可能取值为1.2.3 5分
且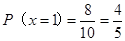 6分
6分 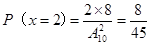 7
7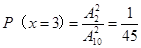 8分
8分
则 的分布列如下表:
的分布列如下表:
10分X 1 2 3 p 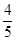
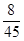
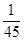
 12分
12分
考点:1.古典概型;2.离散型随机变量的分布列与期望;3.独立重复试验.

练习册系列答案
相关题目
为了调查学生的视力情况,随机抽查了一部分学生的视力,将调查结果分组,分组区间为 ,经过数据处理,得到如下频率分布表
,经过数据处理,得到如下频率分布表
| 分组 | 频数 | 频率 |
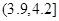 | 3 | 0.06 |
 | 6 | 0.12 |
 | 25 | 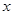 |
 | 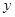 | 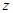 |
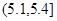 | 2 | 0.04 |
| 合计 | 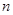 | 1.00 |
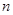 ,
,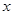 ,
,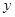 ,
,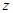 的值
的值(Ⅱ)从样本中视力在
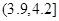 和
和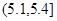 的所有同学中随机抽取两人,求两人视力差的绝对值低于
的所有同学中随机抽取两人,求两人视力差的绝对值低于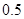 的概率
的概率 某小组共有 、
、 、
、 、
、 、
、 五位同学,他们的身高(单位:米)以及体重指
五位同学,他们的身高(单位:米)以及体重指
标(单位:千克/米2)如下表所示:
| |  |  |  |  |  |
| 身高 |  |  |  |  |  |
| 体重指标 |  |  |  |  |  |
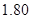 的同学中任选
的同学中任选 人,求选到的
人,求选到的 人身高都在
人身高都在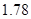 以下的概率;
以下的概率;(2)从该小组同学中任选
 人,求选到的
人,求选到的 人的身高都在
人的身高都在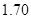 以上且体重指标都在
以上且体重指标都在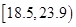 中的概率.
中的概率.  .
. 的概率分布列及期望.
的概率分布列及期望.
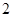 个白球和
个白球和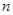 个红球
个红球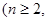 且
且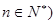 ,每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
,每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.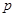 ;
;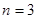 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;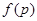 ,当
,当