题目内容
设A(a,1),B(2,b),C(4,5)为坐标平面上三点,O为坐标原点,若 与
与 在
在 方向上的投影相同,则a与b满足的关系式为________.
方向上的投影相同,则a与b满足的关系式为________.
4a-5b=3
分析:构造三个向量,起点是原点,那么三个向量的坐标和点的坐标相同,根据投影的概念,列出等式,用坐标表示,移项整理得到结果.
解答:若 与
与 在
在 方向上的投影相同,而
方向上的投影相同,而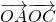 等于
等于 乘以
乘以 在
在 方向上的投影,
方向上的投影,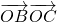 等于
等于 乘以
乘以 在
在 方向上的投影,
方向上的投影,
∴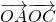 =
=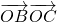 ,即 4a+5=8+5b,∴4a-5b=3,
,即 4a+5=8+5b,∴4a-5b=3,
故答案为 4a-5b=3.
点评:本题主要考查一个向量在另一个向量上的投影的定义,注意投影也是一个数量,不是向量,属于中档题.
分析:构造三个向量,起点是原点,那么三个向量的坐标和点的坐标相同,根据投影的概念,列出等式,用坐标表示,移项整理得到结果.
解答:若
 与
与 在
在 方向上的投影相同,而
方向上的投影相同,而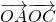 等于
等于 乘以
乘以 在
在 方向上的投影,
方向上的投影,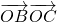 等于
等于 乘以
乘以 在
在 方向上的投影,
方向上的投影,∴
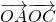 =
=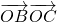 ,即 4a+5=8+5b,∴4a-5b=3,
,即 4a+5=8+5b,∴4a-5b=3,故答案为 4a-5b=3.
点评:本题主要考查一个向量在另一个向量上的投影的定义,注意投影也是一个数量,不是向量,属于中档题.

练习册系列答案
相关题目
设A(a,1),B(2,b),C(4,5)为坐标平面上三点,O为坐标原点,若
与
在
方向上的投影相同,则a与b满足的关系式为( )
| OA |
| OB |
| OC |
| A、4a-5b=3 |
| B、5a-4b=3 |
| C、4a+5b=14 |
| D、5a+4b=14 |