题目内容
设f(x)是定义在R上且周期为2的函数,在区间[-1,1]上,f(x)=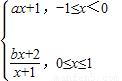 其中a,b∈R.若
其中a,b∈R.若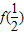 =
=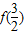 ,则a+3b的值为 .
,则a+3b的值为 .
【答案】分析:由于f(x)是定义在R上且周期为2的函数,由f(x)的表达式可得f( )=f(-
)=f(- )=1-a=f(
)=1-a=f( )=
)=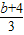 ;再由f(-1)=f(1)得2a+b=0,解关于a,b的方程组可得到a,b的值,从而得到答案.
;再由f(-1)=f(1)得2a+b=0,解关于a,b的方程组可得到a,b的值,从而得到答案.
解答:解:∵f(x)是定义在R上且周期为2的函数,f(x)=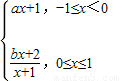 ,
,
∴f( )=f(-
)=f(- )=1-
)=1- a,f(
a,f( )=
)=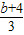 ;又
;又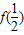 =
=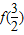 ,
,
∴1- a=
a=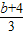 ①
①
又f(-1)=f(1),
∴2a+b=0,②
由①②解得a=2,b=-4;
∴a+3b=-10.
故答案为:-10.
点评:本题考查函数的周期性,考查分段函数的解析式的求法,着重考查方程组思想,得到a,b的方程组并求得a,b的值是关键,属于中档题.
 )=f(-
)=f(- )=1-a=f(
)=1-a=f( )=
)=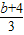 ;再由f(-1)=f(1)得2a+b=0,解关于a,b的方程组可得到a,b的值,从而得到答案.
;再由f(-1)=f(1)得2a+b=0,解关于a,b的方程组可得到a,b的值,从而得到答案.解答:解:∵f(x)是定义在R上且周期为2的函数,f(x)=
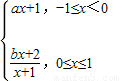 ,
,∴f(
 )=f(-
)=f(- )=1-
)=1- a,f(
a,f( )=
)=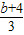 ;又
;又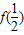 =
=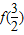 ,
,∴1-
 a=
a=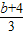 ①
①又f(-1)=f(1),
∴2a+b=0,②
由①②解得a=2,b=-4;
∴a+3b=-10.
故答案为:-10.
点评:本题考查函数的周期性,考查分段函数的解析式的求法,着重考查方程组思想,得到a,b的方程组并求得a,b的值是关键,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x).当x∈[0,2]时,f(x)=2x-x2+a(a是常数).则x∈[2,4]时的解析式为( )
| A、f(x)=-x2+6x-8 | B、f(x)=x2-10x+24 | C、f(x)=x2-6x+8 | D、f(x)=x2-6x+8+a |