题目内容
已知a、b、c分别为三角形ABC的内角A、B、C的对边,向量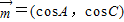 ,
,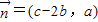 且
且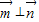 ,则内角A的大小为 .
,则内角A的大小为 .
【答案】分析:根据向量垂直的充要条件得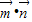 =0,由此建立建立等量关系,并结合正、余弦定理化简整理得cosA=
=0,由此建立建立等量关系,并结合正、余弦定理化简整理得cosA= ,由特殊角的三角函数值即可得到角A的大小.
,由特殊角的三角函数值即可得到角A的大小.
解答:解:∵向量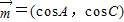 ,
,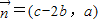 且
且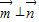 ,
,
∴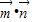 =cosA(c-2b)+acosC=0
=cosA(c-2b)+acosC=0
结合正统定理,得cosA(sinC-2sinB)+sinAcosC=0
∴2sinBcosA=sinAcosC+cosAsinC=sin(A+C)
∵A+C=π-B,
∴sin(A+C)=sinB,得2sinBcosA=sinB,
∵sinB是正数,∴2cosA=1,得cosA=
∵0<A<π,∴A=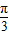
故答案为: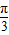
点评:本题给出向量相互垂直,求三角形内角的大小,着重考查了正、余弦定理和平面向量数量积的坐标运算等知识,属于基础题.
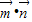 =0,由此建立建立等量关系,并结合正、余弦定理化简整理得cosA=
=0,由此建立建立等量关系,并结合正、余弦定理化简整理得cosA= ,由特殊角的三角函数值即可得到角A的大小.
,由特殊角的三角函数值即可得到角A的大小.解答:解:∵向量
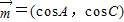 ,
,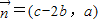 且
且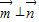 ,
,∴
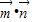 =cosA(c-2b)+acosC=0
=cosA(c-2b)+acosC=0结合正统定理,得cosA(sinC-2sinB)+sinAcosC=0
∴2sinBcosA=sinAcosC+cosAsinC=sin(A+C)
∵A+C=π-B,
∴sin(A+C)=sinB,得2sinBcosA=sinB,
∵sinB是正数,∴2cosA=1,得cosA=

∵0<A<π,∴A=
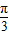
故答案为:
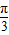
点评:本题给出向量相互垂直,求三角形内角的大小,着重考查了正、余弦定理和平面向量数量积的坐标运算等知识,属于基础题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目