题目内容
【题目】已知函数y=f(x)是定义在R上的奇函数,且当x≥0时,f(x)=-x2+ax.
(1)若a=-2,求函数f(x)的解析式;
(2)若函数f(x)为R上的单调减函数,
①求a的取值范围;
②若对任意实数m,f(m-1)+f(m2+t)<0恒成立,求实数t的取值范围.
【答案】(1) 
.
(2) ①a≤0. ②t> 
.
【解析】
本试题主要是考查了抽象函数的解析式的求解和单调性的证明以及解不等式。
（1）因为当
时，
，又因为
为奇函数，所以
，进而得到解析式。
（2）根据函数单调性，对于参数a分为正负来讨论得到取值范围。
（3）因为
，∴
所以是奇函数，∴
，而又因为为
上的单调递减函数，所以
恒成立，分离参数的思想得到范围。
（1）当时，，又因为为奇函数，
所以
所以
…………………………6分
（2）①当
时，对称轴
，所以
在
上单调递减，
由于奇函数关于原点对称的区间上单调性相同，所以在
上单调递减，
又在上
，在
上
，
所以当a
0时，
为R上的单调递减函数
当a>0时，在
上递增，在
上递减，不合题意
所以函数为单调函数时，a的范围为a
………………………………………….10分
②因为，∴
所以是奇函数，∴…………………………12分
又因为为上的单调递减函数，所以恒成立，…………………14分
所以
恒成立， 所以
…………………………16分
【题目】中国共产党第十九次全国代表大会于2017年10月24日在北京召开，会议提出“决胜全面建成小康社会”.某市积极响应开展“脱贫攻坚”，为2020年“全面建成小康社会”贡献力量.为了解该市农村“脱贫攻坚“情况，从某县调查得到农村居民2011年至2017年家庭人均纯收入
（单位：百元）的数据如下表：
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年人均纯收入 | 41 | 45 | 48 | 56 | 60 | 64 | 71 |
注：小康的标准是农村居民家庭年人均纯收入达到8000元.
（1）求关于
的线性回归方程；
（2）利用（1）中的回归方程，预测2020年该县农村居民家庭年人均纯收入能否达到“全面建成小康社会”的标准？
附：回归直线
的斜率和截距的最小二乘估计公式分别为：
，
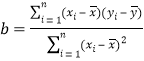