题目内容
若不等式
，对
恒成立， 则关于t的不等式
的解为 ( )
A． | B． |
C． | D． |
A
解析试题分析：∵不等式，对恒成立，∴
，∴0<a<1，又
，∴
，解得1<t<2，故选A
考点：本题考查了不等式的解法
点评：对于指数、对数不等式常常用函数的单调性转化为整式不等式求解
练习册系列答案
相关题目
有甲、乙两个粮食经销商每次在同一粮食生产地以相同的价格购进粮食，他们共购进粮食两次，各次的粮食价格不同，甲每次购粮10000千克，乙每次购粮食10000元，在两次统计中，购粮的平均价格较低的是（ ）
| A．甲 | B．乙 | C．一样低 | D．不确定 |
已知不等式ax2－bx－1≥0的解集是，则不等式x2－bx－a＜0的解集是( )．
| A．(2,3) | B．(－∞，2)∪(3，＋∞) |
| C． | D．∪ |
不等式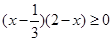
的解集是
A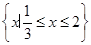． | B． |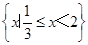
C． | D． |
不等式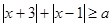
对任意实数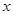
恒成立，则实数
的取值范围是（ ）
A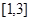． | B． | C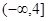． | D． |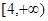
若定义在R上的函数f(x)满足
,且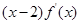
<0，a="f" (
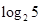),b="f" (
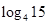),c="f" (
)，则a,b,c的大小关系为
| A．a>b>c | B．c>b>a | C．b>a>c | D．c>a>b |
不等式
的解集为（ ）
A． | B． |
C． | D． |
的解集为______________________。不等式
的解集为( )
A． | B． | C． | D． |