题目内容
与曲线ρcosθ+1=0关于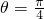
对称的曲线的极坐标方程是________．
ρsinθ+1=0
分析：先将原极坐标方程ρcosθ+1=0化成直角坐标方程，再结合曲线关于直线的对称性，利用直角坐标方程解决问题．
解答：将原极坐标方程ρcosθ+1=0，
化成直角坐标方程为：x+1=0，
它关于直线y=x（即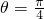）对称的圆的方程是
y+1=0，其极坐标方程为：ρsinθ+1=0
故答案为：ρsinθ+1=0．
点评：本题考查点的极坐标和直角坐标的互化，利用直角坐标与极坐标间的关系：ρcosθ=x，ρsinθ=y，ρ2=x2+y2，进行代换即得．
分析：先将原极坐标方程ρcosθ+1=0化成直角坐标方程，再结合曲线关于直线的对称性，利用直角坐标方程解决问题．
解答：将原极坐标方程ρcosθ+1=0，
化成直角坐标方程为：x+1=0，
它关于直线y=x（即
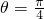）对称的圆的方程是y+1=0，其极坐标方程为：ρsinθ+1=0
故答案为：ρsinθ+1=0．
点评：本题考查点的极坐标和直角坐标的互化，利用直角坐标与极坐标间的关系：ρcosθ=x，ρsinθ=y，ρ2=x2+y2，进行代换即得．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目