题目内容
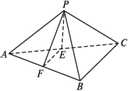
已知如下图,三棱锥P-ABC中,PA⊥平面ABC,PA=AB,AC=BC=1,∠ACB=90°,点E与点F分别在PA与PB上,且![]() ,
,![]() ,M是PB的中点.
,M是PB的中点.
(1)求证:BC⊥PC;
(2)求异面直线EF与MC所成的角;
(3)求直线MC与底面ABC所成的角.

答案:
解析:
解析:
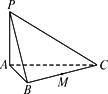
(1)证明:∵ ∴ 又∵ (2)解:连结 ∴ 在 由 ∵ 在Rt△ 即所求异面直线 (3)解:如下图,∵ ∴ 在平面 由 在 ∴
|

练习册系列答案
相关题目
 ,
,