题目内容
已知二次函数![]() ),满足
),满足![]() 且f(x)的最小值是-
且f(x)的最小值是-![]() .设数列{an}的前n项和为Sn,对一切n∈N*,点(n,Sn)在函数f(x)的图象上.
.设数列{an}的前n项和为Sn,对一切n∈N*,点(n,Sn)在函数f(x)的图象上.
(1)求数列{an}的通项公式;
(2)通过![]() 造一个新的数列{bn},是否存在非零常数c,使得{bn}为等差数列;
造一个新的数列{bn},是否存在非零常数c,使得{bn}为等差数列;
(3)令![]() ,设数列{cn·2cn}的前n项和为Tn,求Tn.
,设数列{cn·2cn}的前n项和为Tn,求Tn.
解:(1)因为f(0)=f(![]() )=0,
)=0,
所以f(x)的对称轴为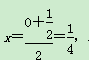
又因为f(x)的最小值是-![]() ,
,
由二次函数图象的对称性可设:
![]() 又f(0)=0,所以a=2,
又f(0)=0,所以a=2,
所以![]()
因为点(n,Sn)在函数f(x)的图象上,
所以Sn=2n2-n.
当n=1时,a1=S1=1;
当n≥2时,an=Sn-Sn-1=4n-3(n=1时也成立),
![]() 所以an=4n-3(n∈N*).
所以an=4n-3(n∈N*).
(2)因为![]()
(3),即得bn=2n,此时数列{bn}为等差数列,所以存在非零常数c=-![]() ,使得{bn}为等差数列.
,使得{bn}为等差数列.
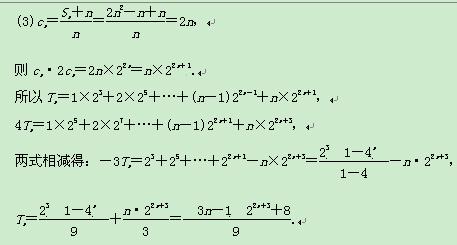

练习册系列答案
相关题目
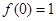 ,
,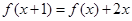
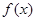
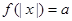
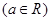 的解的个数
的解的个数 对
对 都满足
都满足 且
且 ,设函数
,设函数
 ,
, ).
). ,使
,使 成立,求实数
成立,求实数 的取值范围;
的取值范围;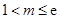 ,
, ,求证:对于
,求证:对于 ,恒有
,恒有 .
.  .
.  ;
; 的解的个数.
的解的个数.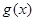 对
对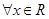 都满足
都满足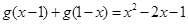 且
且 ,设函数
,设函数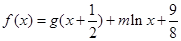 (
(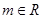 ,
,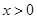 ).
). ,使
,使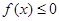 成立,求实数
成立,求实数 的取值范围;
的取值范围; 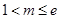 ,
,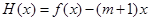 ,求证:对于
,求证:对于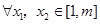 ,恒有
,恒有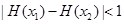 .
.