题目内容
如图:在三棱柱ABC-A1B1C1中,底面正三角形ABC的边长为3,D为侧棱BB1的中点,且DB=2,∠ABD=90°,DA=DC.
(1)证明:平面AC1D⊥平面AA1C1C;
(2)求三棱锥A1-AC1D的体积.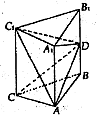
(1)证明:平面AC1D⊥平面AA1C1C;
(2)求三棱锥A1-AC1D的体积.

(1)证明:∵DA=DC,DB=DB,BA=BC,
∴△ABD≌△CBD,
∴∠ABD=∠CBD=90°,即DB⊥BA,DB⊥BC,又BA∩BC=B,
∴DB⊥平面ABC,即BB1⊥
∴CC1⊥平面ABC,…4分
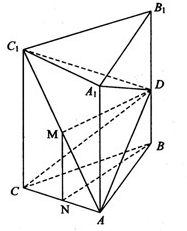
设AC1的中点为M,AC的中点为N,连接DM、DN和BN,则MN∥CC1且MN=
CC1,
又∵BD∥CC1且BD=
CC1,
∴MN
BD,即四边形MNBD为平行四边形,
∴MD∥BN,又△ABC为正三角形,
∴BN⊥AC,
又∵CC1⊥平面ABC,
∴CC1⊥BN,又CC1∩CA=C,
∴BN⊥平面AA1C1C,
∴DM⊥平面AA1C1C,
又DM⊆平面AC1D,
∴平面AC1D⊥平面AA1C1C;…9分
(2)∵△AA1C1的面积为6,
∴三棱锥A1-AC1D的体积V=
×6×DM=2BN=3
…12分
∴△ABD≌△CBD,
∴∠ABD=∠CBD=90°,即DB⊥BA,DB⊥BC,又BA∩BC=B,
∴DB⊥平面ABC,即BB1⊥
∴CC1⊥平面ABC,…4分

设AC1的中点为M,AC的中点为N,连接DM、DN和BN,则MN∥CC1且MN=
| 1 |
| 2 |
又∵BD∥CC1且BD=
| 1 |
| 2 |
∴MN
| ∥ |
| . |
∴MD∥BN,又△ABC为正三角形,
∴BN⊥AC,
又∵CC1⊥平面ABC,
∴CC1⊥BN,又CC1∩CA=C,
∴BN⊥平面AA1C1C,
∴DM⊥平面AA1C1C,
又DM⊆平面AC1D,
∴平面AC1D⊥平面AA1C1C;…9分
(2)∵△AA1C1的面积为6,
∴三棱锥A1-AC1D的体积V=
| 1 |
| 3 |
| 3 |

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )
如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )| A、3:2 | B、7:5 | C、8:5 | D、9:5 |
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,A1A=AC=2,BC=1,AB=
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,A1A=AC=2,BC=1,AB= 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3 (2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2
(2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2 如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.
如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.