题目内容
已知向量 ,
, 满足|
满足| |=|
|=| |=|
|=| +
+ |=1,则向量
|=1,则向量 ,
, 夹角的余弦值为
夹角的余弦值为
- A.

- B.-

- C.

- D.-

B
分析:将| +
+ |=1两边平方,结合已知条件可算出
|=1两边平方,结合已知条件可算出 •
• =-
=- ,再用两个向量的夹角公式即可算出向量
,再用两个向量的夹角公式即可算出向量 ,
, 夹角的余弦值.
夹角的余弦值.
解答:∵| +
+ |=1,
|=1,
∴( +
+ )2=
)2= 2+2
2+2 •
• +
+ 2=1
2=1
∵| |=|
|=| |=1,得
|=1,得 2=
2= 2=1
2=1
∴代入上式得:2 •
• =-1,
=-1, •
• =-
=-
因此,向量 ,
, 夹角的余弦为cosθ=
夹角的余弦为cosθ= =-
=-
故选:B
点评:本题给出向量 、
、 满足的条件,求它们夹角的余弦之值,着重考查了平面向量数量积的公式及其运算性质等知识,属于基础题.
满足的条件,求它们夹角的余弦之值,着重考查了平面向量数量积的公式及其运算性质等知识,属于基础题.
分析:将|
 +
+ |=1两边平方,结合已知条件可算出
|=1两边平方,结合已知条件可算出 •
• =-
=- ,再用两个向量的夹角公式即可算出向量
,再用两个向量的夹角公式即可算出向量 ,
, 夹角的余弦值.
夹角的余弦值.解答:∵|
 +
+ |=1,
|=1,∴(
 +
+ )2=
)2= 2+2
2+2 •
• +
+ 2=1
2=1∵|
 |=|
|=| |=1,得
|=1,得 2=
2= 2=1
2=1∴代入上式得:2
 •
• =-1,
=-1, •
• =-
=-
因此,向量
 ,
, 夹角的余弦为cosθ=
夹角的余弦为cosθ= =-
=-
故选:B
点评:本题给出向量
 、
、 满足的条件,求它们夹角的余弦之值,着重考查了平面向量数量积的公式及其运算性质等知识,属于基础题.
满足的条件,求它们夹角的余弦之值,着重考查了平面向量数量积的公式及其运算性质等知识,属于基础题. 
练习册系列答案
相关题目
 、
、 满足
满足 ,则
,则 .
. ,实数
,实数 满足
满足 ,则
,则 的最小值为( )
的最小值为( ) B.1 C.
B.1 C. D.
D.
 ,
, 满足
满足 ,
, ,
, ,则
,则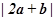 的值为_______.
的值为_______.