题目内容
已知直线 :
: 为参数), 曲线
为参数), 曲线
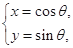 (
( 为参数).
为参数).
(1)设 与
与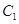 相交于
相交于 两点,求
两点,求 ;
;
(2)若把曲线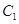 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的 倍,得到曲线
倍,得到曲线 ,设点
,设点 是曲线
是曲线 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值.
(1) ;(2)
;(2) .
.
解析试题分析:本题考查直角坐标系与极坐标系之间的互化、参数方程的几何意义、三角函数的值域、函数图像的平移等基础知识,考查学生的转化能力和计算能力.第一问,由参数方程和普通方程的互化公式消参得出 和
和 的普通方程,由于两图像相交,所以联立求交点,再利用两点间距离公式求
的普通方程,由于两图像相交,所以联立求交点,再利用两点间距离公式求 ;第二问,根据已知先得到曲线
;第二问,根据已知先得到曲线 的参数方程,写出点P的坐标,利用点到直线的距离公式求距离,再利用三角函数的有界性求函数的最值.
的参数方程,写出点P的坐标,利用点到直线的距离公式求距离,再利用三角函数的有界性求函数的最值.
试题解析:(1) 的普通方程为
的普通方程为 的普通方程为
的普通方程为
联立方程组 解得
解得 与
与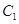 的交点为
的交点为 ,
, ,
,
则 .
.
(2) 的参数方程为
的参数方程为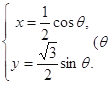 为参数).故点
为参数).故点 的坐标是
的坐标是 ,
,
从而点 到直线
到直线 的距离是
的距离是 ,
,
由此当 时,
时, 取得最小值,且最小值为
取得最小值,且最小值为 .
.
考点:1.参数方程与普通方程的互化;2.函数图像的平移;3.点到直线的距离公式.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 的直角坐标方程为
的直角坐标方程为 . 以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系. P是曲线
. 以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系. P是曲线 ,
, ,将点P绕点O逆时针旋转角
,将点P绕点O逆时针旋转角 后得到点Q,
后得到点Q, ,点M的轨迹是曲线
,点M的轨迹是曲线 .
. 的取值范围.
的取值范围. 的直线与圆
的直线与圆 :
: 的一个交点为
的一个交点为 ,点
,点 为线段
为线段 的中点。
的中点。 (t为参数)和圆C的极坐标方程:ρ=2
(t为参数)和圆C的极坐标方程:ρ=2 sin(θ+
sin(θ+ ),判断直线和圆C的位置关系.
),判断直线和圆C的位置关系. ρcos(θ-
ρcos(θ- )=2.
)=2. .
. 的参数方程为
的参数方程为 (t为参数),直线
(t为参数),直线 ,求|MA|·|MB|.
,求|MA|·|MB|. 中,圆
中,圆 的参数方程
的参数方程 为参数).以
为参数).以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系. 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆
与圆 ,与直线
,与直线 ,求线段
,求线段 的长.
的长. 到直线ρsinθ=2的距离.
到直线ρsinθ=2的距离. =2
=2 .
. (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.