题目内容
【题目】设函数![]() (
(![]() ),
),![]() ,
,
(Ⅰ) 试求曲线![]() 在点
在点![]() 处的切线l与曲线
处的切线l与曲线![]() 的公共点个数;(Ⅱ) 若函数
的公共点个数;(Ⅱ) 若函数![]() 有两个极值点,求实数a的取值范围.
有两个极值点,求实数a的取值范围.
(附:当![]() ,x趋近于0时,
,x趋近于0时, ![]() 趋向于
趋向于![]() )
)
【答案】(1)两个公共点;(2)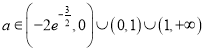 .
.
【解析】试题分析:(1)计算出![]() 及
及![]() ,根据点斜式可得切线方程,将切线方程与
,根据点斜式可得切线方程,将切线方程与![]() 联立可得方程
联立可得方程![]() ,设
,设![]() ,对其求导,可得其在
,对其求导,可得其在![]() 内的单调性,结合
内的单调性,结合![]() ,
, ![]() ,可得零点个数;(2)题意等价于
,可得零点个数;(2)题意等价于![]() 在
在![]() 至少有两不同根,当
至少有两不同根,当![]() 时,
时, ![]() 是
是![]() 的根,根据图象的交点可知
的根,根据图象的交点可知![]() 有一个零点,除去同根;当
有一个零点,除去同根;当![]() 显然不合题意;当
显然不合题意;当![]() 时,题意等价于
时,题意等价于![]() 在
在![]() 至少有两不同根,对其求导判断单调性,考虑极值与两端的极限值可得结果.
至少有两不同根,对其求导判断单调性,考虑极值与两端的极限值可得结果.
试题解析:(1)∵![]() ,
, ![]() ,
,
切线![]() 的斜率为
的斜率为![]() ,
,
∴切线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
联立![]() ,得
,得![]() ;
;
设![]() ,则
,则![]() ,
,
由![]() 及
及![]() ,得
,得![]() 或
或![]() ,
,
∴![]() 在
在![]() 和
和![]() 上单调递增,可知
上单调递增,可知![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,
, ![]() ,所以
,所以![]() ,
, ![]() ,
,
∴方程![]() 有两个根:1和
有两个根:1和![]() ,从而切线
,从而切线![]() 与曲线
与曲线![]() 有两个公共点.
有两个公共点.
(2)由题意知![]() 在
在![]() 至少有两不同根,
至少有两不同根,
设![]() ,
,
①当![]() 时,
时, ![]() 是
是![]() 的根,
的根,
由![]() 与
与![]() (
(![]() )恰有一个公共点,可知
)恰有一个公共点,可知![]() 恰有一根
恰有一根![]() ,
,
由![]() 得
得![]() ,不合题意,
,不合题意,
∴当![]() 且
且![]() 时,检验可知
时,检验可知![]() 和
和![]() 是
是![]() 的两个极值点;
的两个极值点;
②当![]() 时,
时, ![]() 在
在![]() 仅一根,所以
仅一根,所以![]() 不合题意;--9分
不合题意;--9分
③当![]() 时,需
时,需![]() 在
在![]() 至少有两不同根,
至少有两不同根,
由![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
可知![]() 在
在![]() 上单调递减,
上单调递减,
因为![]() ,
, ![]() 趋近于0时,
趋近于0时, ![]() 趋向于
趋向于![]() ,且
,且![]() 时,
时, ![]() ,
,
由题意知,需![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴![]() .
.
综上知, 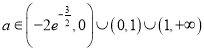 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


