题目内容
设函数 ,其中向量
,其中向量 ,x∈R,且
,x∈R,且 .
.
(Ⅰ)求实数m的值;
(Ⅱ)求函数f(x)在区间 上的最大值.
上的最大值.
解:(Ⅰ) .(3分)
.(3分)
由 ,得m=1. (5分)
,得m=1. (5分)
(Ⅱ)由(Ⅰ)得 .(8分)
.(8分)
由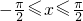 ,得
,得 .
.
∴当 ,即
,即 时,函数f(x)有最大值
时,函数f(x)有最大值 .(12分)
.(12分)
分析:(I)由已知中向量 ,函数
,函数 ,根据向量数量积运算法则,我们易求出函数的解析式,结合
,根据向量数量积运算法则,我们易求出函数的解析式,结合 ,我们可以构造一个关于m的方程,进而求出m的值.
,我们可以构造一个关于m的方程,进而求出m的值.
(II)由(I)中结论,我们可以求出函数f(x)的解析式,利用辅助角公式,我们可将其化为正弦型函数的形式,进而根据正弦型函数的性质,求出函数f(x)在区间 上的最大值.
上的最大值.
点评:本题考查的知识点是三角函数的最值,平面向量数量积的运算,其中(I)的关键是根据平面向量数量积的运算公式,结合 ,构造一个关于m的方程,(II)的关键是辅助角公式,将函数f(x)的解析式化为正弦型函数的形式.
,构造一个关于m的方程,(II)的关键是辅助角公式,将函数f(x)的解析式化为正弦型函数的形式.
 .(3分)
.(3分)由
 ,得m=1. (5分)
,得m=1. (5分)(Ⅱ)由(Ⅰ)得
 .(8分)
.(8分)由
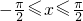 ,得
,得 .
.∴当
 ,即
,即 时,函数f(x)有最大值
时,函数f(x)有最大值 .(12分)
.(12分)分析:(I)由已知中向量
 ,函数
,函数 ,根据向量数量积运算法则,我们易求出函数的解析式,结合
,根据向量数量积运算法则,我们易求出函数的解析式,结合 ,我们可以构造一个关于m的方程,进而求出m的值.
,我们可以构造一个关于m的方程,进而求出m的值.(II)由(I)中结论,我们可以求出函数f(x)的解析式,利用辅助角公式,我们可将其化为正弦型函数的形式,进而根据正弦型函数的性质,求出函数f(x)在区间
 上的最大值.
上的最大值.点评:本题考查的知识点是三角函数的最值,平面向量数量积的运算,其中(I)的关键是根据平面向量数量积的运算公式,结合
 ,构造一个关于m的方程,(II)的关键是辅助角公式,将函数f(x)的解析式化为正弦型函数的形式.
,构造一个关于m的方程,(II)的关键是辅助角公式,将函数f(x)的解析式化为正弦型函数的形式. 
练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
 ,其中向量
,其中向量 ,x∈R,且
,x∈R,且 .
.  上的最大值.
上的最大值. ,其中向量
,其中向量 =(m,cos2x),
=(m,cos2x), =(1+sin2x,1),x∈R,且y=f(x)的图象经过点
=(1+sin2x,1),x∈R,且y=f(x)的图象经过点 .
. ,其中向量
,其中向量 =(m,cos2x),
=(m,cos2x), =(1+sin2x,1),x∈R,且y=f(x)的图象经过点
=(1+sin2x,1),x∈R,且y=f(x)的图象经过点 .
. ,其中向量
,其中向量 =(m,cos2x),
=(m,cos2x), =(1+sin2x,1),x∈R,且y=f(x)的图象经过点
=(1+sin2x,1),x∈R,且y=f(x)的图象经过点 .
.