题目内容
已知函数f(x)=1-sinx.(1)用五点法作出f(x)在一个周期[0,2π]的图象;(要求列表)
(2)已知g(x)=f(x+
 ),求出g(x)在整个定义域内的最大最小值及相应的x值,并写出g(x)的单调递增区间.
),求出g(x)在整个定义域内的最大最小值及相应的x值,并写出g(x)的单调递增区间.
【答案】分析:(1)列出表格,描出五个关键点,连接即可得到草图;
(2)分别令x+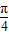 =2kπ+
=2kπ+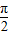 ,x+
,x+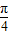 =2kπ-
=2kπ-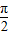 ,k∈Z,可求得x值及相应函数最值;由2kπ
,k∈Z,可求得x值及相应函数最值;由2kπ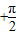 ≤x+
≤x+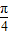 ≤2kπ+
≤2kπ+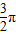 ,可得求得g(x)的增区间;
,可得求得g(x)的增区间;
解答:解:(1)列表如下:
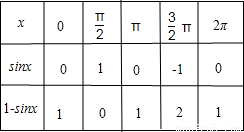
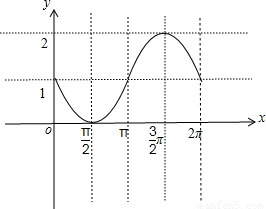 描出五个关键点(0,1),(
描出五个关键点(0,1),(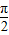 ,0),(π,1),(
,0),(π,1),(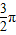 ,2),(2π,0),
,2),(2π,0),
连接成线即可得到f(x)的草图,如右图所示:
(2)g(x)=f(x+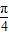 )=1-sin(x+
)=1-sin(x+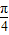 ),
),
当x+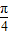 =2kπ+
=2kπ+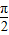 ,即x=2k
,即x=2k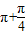 (k∈Z)时,g(x)取得最小值0;
(k∈Z)时,g(x)取得最小值0;
当x+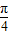 =2kπ-
=2kπ-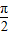 ,即x=2kπ-
,即x=2kπ-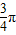 (k∈Z)时,g(x)取得最大值2;
(k∈Z)时,g(x)取得最大值2;
由2kπ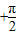 ≤x+
≤x+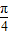 ≤2kπ+
≤2kπ+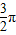 ,得2kπ
,得2kπ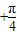 ≤x≤2kπ
≤x≤2kπ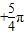 ,k∈Z,
,k∈Z,
所以g(x)的增区间为[2kπ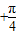 ,2kπ
,2kπ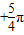 ](k∈Z).
](k∈Z).
点评:本题考查五点法作图、函数的图象变换、正弦函数的单调性等知识,考查学生对知识的应用能力.
(2)分别令x+
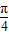 =2kπ+
=2kπ+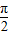 ,x+
,x+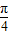 =2kπ-
=2kπ-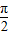 ,k∈Z,可求得x值及相应函数最值;由2kπ
,k∈Z,可求得x值及相应函数最值;由2kπ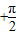 ≤x+
≤x+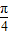 ≤2kπ+
≤2kπ+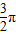 ,可得求得g(x)的增区间;
,可得求得g(x)的增区间;解答:解:(1)列表如下:

 描出五个关键点(0,1),(
描出五个关键点(0,1),(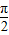 ,0),(π,1),(
,0),(π,1),(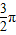 ,2),(2π,0),
,2),(2π,0),连接成线即可得到f(x)的草图,如右图所示:
(2)g(x)=f(x+
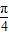 )=1-sin(x+
)=1-sin(x+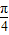 ),
),当x+
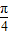 =2kπ+
=2kπ+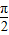 ,即x=2k
,即x=2k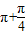 (k∈Z)时,g(x)取得最小值0;
(k∈Z)时,g(x)取得最小值0;当x+
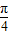 =2kπ-
=2kπ-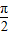 ,即x=2kπ-
,即x=2kπ-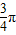 (k∈Z)时,g(x)取得最大值2;
(k∈Z)时,g(x)取得最大值2;由2kπ
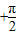 ≤x+
≤x+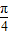 ≤2kπ+
≤2kπ+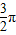 ,得2kπ
,得2kπ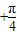 ≤x≤2kπ
≤x≤2kπ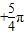 ,k∈Z,
,k∈Z,所以g(x)的增区间为[2kπ
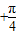 ,2kπ
,2kπ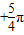 ](k∈Z).
](k∈Z).点评:本题考查五点法作图、函数的图象变换、正弦函数的单调性等知识,考查学生对知识的应用能力.

练习册系列答案
相关题目
已知函数f(x)=
,g(x)=1+
,若f(x)>g(x),则实数x的取值范围是( )
| 1 |
| |x| |
| x+|x| |
| 2 |
| A、(-∞,-1)∪(0,1) | ||||
B、(-∞,-1)∪(0,
| ||||
C、(-1,0)∪(
| ||||
D、(-1,0)∪(0,
|