题目内容
已知函数f(x)=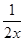 -cosx,若
-cosx,若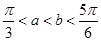 ,则( )
,则( )
| A.f(a)>f(b) | B.f(a)<f(b) | C.f(a)=f(b) | D.f(a)f(b)>0 |
B
解析试题分析: ,当
,当 时,
时, ,
, ,则当
,则当 时,
时, ,即函数
,即函数 在
在 单调递增,即
单调递增,即 .
.
考点:1.利用导数判断函数的单调性;2.利用函数的单调性比较大小.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
设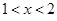 ,则
,则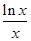 、
、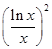 、
、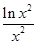 的大小关系是( )
的大小关系是( )
A. | B.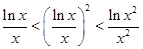 |
C.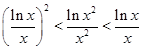 | D.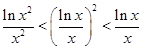 |
曲线 与
与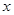 轴以及直线
轴以及直线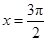 所围图形的面积为( )
所围图形的面积为( )
A.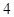 | B.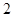 | C.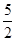 | D.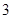 |
曲线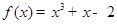 在
在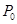 处的切线平行于直线
处的切线平行于直线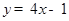 ,则
,则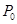 点的坐标为( )
点的坐标为( )
A.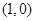 | B.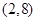 |
C.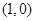 和 和 | D.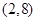 和 和 |
函数 的单调递减区间为( )
的单调递减区间为( )
A.( 1,1) 1,1) | B.(0,1] | C.[1,+∞) | D.( ∞,-1)∪(0,1] ∞,-1)∪(0,1] |
设底为等边三角形的直棱柱的体积为V,那么其表面积最小时,底面边
长为( )
A.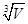 | B.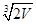 | C.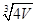 | D.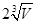 |
已知函数f(x)在x=1处的导数为3,则f(x)的解析式可能为 ( ).
| A.f(x)=(x-1)2+3(x-1) |
| B.f(x)=2(x-1) |
| C.f(x)=2(x-1)2 |
| D.f(x)=x-1 |
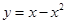 与x轴所围成的平面区域为
与x轴所围成的平面区域为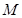 ,该抛物线与直线y=
,该抛物线与直线y=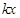 (k>0)所围成的平面区域为
(k>0)所围成的平面区域为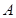 ,向区域
,向区域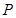 ,若点
,若点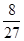 ,则k的值为( )
,则k的值为( )
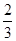
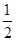
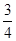
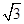 ),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )
),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )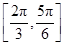
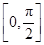 ∪
∪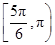
 ∪
∪