题目内容
(本小题满分10分)选修4－4：坐标系与参数方程
已知极坐标的极点在平面直角坐标系的原点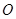
处，极轴与
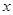轴的正半轴重合，且长度单位相同．直线
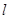的极坐标方程为：
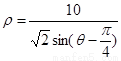,点
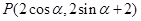，参数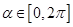
.
(Ⅰ)求点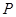
轨迹的直角坐标方程；
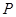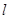(Ⅱ)求点到直线距离的最大值.
【答案】
(Ⅰ)点
的轨迹方程为
．
(Ⅱ)点到直线
距离的最大值
.
【解析】（1）利用平方关系消去参数
就得到点的轨迹方程为．
（2）先把直线的极坐标方程为：
化为直角坐标方程为
．点到直线距离的最大值就是圆心到直线的距离加上半径.
(Ⅰ)
且参数
，
所以点的轨迹方程为．······················································· 3分
(Ⅱ)因为，所以
，
所以
，所以直线的直角坐标方程为．········ 6分
法一：由(Ⅰ) 点的轨迹方程为，圆心为
，半径为2.
，所以点到直线距离的最大值.··········· 10分
法二：
，当
，
，即点到直线距离的最大值.··························································································· 10分
练习册系列答案
阅读快车系列答案
相关题目
（选做题）本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，若多做，则按作答的前两题评分，解答时应写出文字说明、证明过程或演算步骤．
本题包括（1）、（2）、（3）、（4）四小题，请选定其中两题，并在答题卡指定区域内答，