题目内容
已知抛物线关于坐标轴对称.顶点为坐标原点,并且经过点M(
思路分析:抛物线为标准方程,可设成y2=2px(p≠0),用待定系数法求解.?
解:因为抛物线关于坐标轴对称,顶点为坐标原点,所以应分两种情况:焦点在x轴上,可设其方程为y2=2px(p≠0);焦点在y轴上,可设其方程为x2=2my(m≠0).?
又抛物线经过点M(![]() ,-2
,-2![]() ),?
),?
∴(-2![]() )2=2p(
)2=2p(![]() ),∴p=2
),∴p=2![]() ;?
;?
或(![]() )2=2m(-2
)2=2m(-2![]() ),∴m=-
),∴m=-![]() .?
.?
故所求方程为y2=4![]() x或x2=-
x或x2=-![]() y.?
y.?
这样的抛物线共两条,一条开口向右,一条开口向下.
温馨提示
不知抛物线开口方向时,可设参数p≠0,而不知对称轴为何轴时,研究方程应分两种情形.

练习册系列答案
相关题目
 ),N(-
),N(- ,
, ),且抛物线与椭圆交于两点A(xA,yA)和B(xB,yB),且xA<xB.
),且抛物线与椭圆交于两点A(xA,yA)和B(xB,yB),且xA<xB. =0恒有公共点,试求m的取值范围.
=0恒有公共点,试求m的取值范围.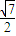 ),N(-
),N(-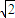 ,
,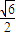 ),且抛物线与椭圆交于两点A(xA,yA)和B(xB,yB),且xA<xB.
),且抛物线与椭圆交于两点A(xA,yA)和B(xB,yB),且xA<xB.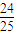 =0恒有公共点,试求m的取值范围.
=0恒有公共点,试求m的取值范围.