题目内容
 在直三棱柱ABC-A1B1C1中A1A=
在直三棱柱ABC-A1B1C1中A1A=| 3 |
(Ⅰ)求证:AB⊥平面A1ACC1;
(Ⅱ)求证:A1B∥平面AC1D.
分析:(Ⅰ)欲证AB⊥平面A1ACC1,根据直线与平面垂直的判定定理可知只需证AB与平面A1ACC1内两相交直线垂直,利用勾股定理可得AB⊥AC,A1A⊥AB,A1A∩AC=A,满足定理条件;
(Ⅱ)连接A1C交AC1于E,连DE,则E为A1C中点,欲证A1B∥平面AC1D,根据直线与平面平行的判定定理可知只需证A1B∥平面AC1D内一直线平行,而DE∥A1B,A1B?平面AC1D,DE?平面AC1D,满足定理条件.
(Ⅱ)连接A1C交AC1于E,连DE,则E为A1C中点,欲证A1B∥平面AC1D,根据直线与平面平行的判定定理可知只需证A1B∥平面AC1D内一直线平行,而DE∥A1B,A1B?平面AC1D,DE?平面AC1D,满足定理条件.
解答: 证明:(Ⅰ)在△ABC中,AC=
证明:(Ⅰ)在△ABC中,AC=
=
∴AB2+AC2=BC2
∴AB⊥AC
∵直三棱柱ABC-A1B1C1
∴A1A⊥平面ABC,
∴A1A⊥AB
又∵A1A∩AC=A
∴AB⊥平面A1ACC1,
(Ⅱ)连接A1C交AC1于E,连DE,则E为A1C中点.
∴DE∥A1B
又∵A1B?平面AC1D,DE?平面AC1D
∴A1B∥平面AC1D
 证明:(Ⅰ)在△ABC中,AC=
证明:(Ⅰ)在△ABC中,AC=| AB2+BC2-2AB•BCcos∠ABC |
| 3 |
∴AB2+AC2=BC2
∴AB⊥AC
∵直三棱柱ABC-A1B1C1
∴A1A⊥平面ABC,
∴A1A⊥AB
又∵A1A∩AC=A
∴AB⊥平面A1ACC1,
(Ⅱ)连接A1C交AC1于E,连DE,则E为A1C中点.
∴DE∥A1B
又∵A1B?平面AC1D,DE?平面AC1D
∴A1B∥平面AC1D
点评:本题主要考查了直线与平面垂直的判定,以及直线与平面平行的判定,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
相关题目
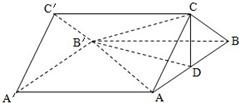 如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点.
如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点. (2012•泸州一模)如图,在直三棱柱ABC-A′B′C′中,AB=BC=CA=a,
(2012•泸州一模)如图,在直三棱柱ABC-A′B′C′中,AB=BC=CA=a, 如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数).
如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数). 如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角.
如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角. 如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,
如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,