题目内容
 已知函数f(x)=
已知函数f(x)=
|
(1)画出函数y=f(x)的简图(要求标出关键的点、线);
(2)结合图象,求当f(x)>1时,x的取值范围;
(3)观察图象,若关于x的方程f(x)=t有两个解,求实数 t的取值范围.
分析:(1)根据指数函数的图象和性质,一次函数的图象和性质及对数函数的图象和性质,进而根据分段函数分段画的原则,可得函数y=f(x)的简图;
(2)令-4x+3=1得x=
;令log
(x-1)=1得x=
,进而根据(1)中图象,可得当f(x)>1时,x的取值范围;
(3)若关于x的方程f(x)=t有两个解,即函数y=f(x)的图象与直线y=t只有两个交点,进而根据(1)中图象,可得实数 t的取值范围.
(2)令-4x+3=1得x=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
(3)若关于x的方程f(x)=t有两个解,即函数y=f(x)的图象与直线y=t只有两个交点,进而根据(1)中图象,可得实数 t的取值范围.
解答:解:(1)函数f(x)=
的图象如下图所示:
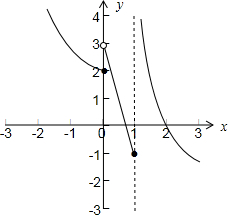
(2)因为(
)x+1>1恒成立;
令-4x+3=1得x=
;
令log
(x-1)=1得x=
结合图象观察,f(x)>1时的x的取值范围是:x<
或1<x<
(3)观察图象知,方程f(x)=t有两个解等价于
函数y=f(x)的图象与直线y=t只有两个交点.
所以实数 t的取值范围是-1≤t<2或t≥3
|
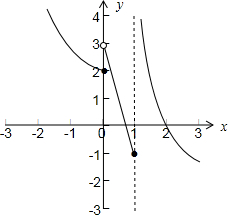
(2)因为(
| 1 |
| 2 |
令-4x+3=1得x=
| 1 |
| 2 |
令log
| 1 |
| 2 |
| 3 |
| 2 |
结合图象观察,f(x)>1时的x的取值范围是:x<
| 1 |
| 2 |
| 3 |
| 2 |
(3)观察图象知,方程f(x)=t有两个解等价于
函数y=f(x)的图象与直线y=t只有两个交点.
所以实数 t的取值范围是-1≤t<2或t≥3
点评:本题考查的知识点是分段函数的图象,熟练掌握指数函数的图象和性质,一次函数的图象和性质及对数函数的图象和性质,是解答的关键.

练习册系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|