题目内容
函数![]() 的定义域为集合
的定义域为集合![]() ,函数
,函数![]() 的定义域为集合
的定义域为集合![]() . (1)判定函数
. (1)判定函数![]() 的奇偶性,并说明理由.
的奇偶性,并说明理由.
(2)问:![]() 是
是![]() 的什么条件(充分非必要条件 、必要非充分条件、充要条件、既非充分也非必要条件)? 并证明你的结论.
的什么条件(充分非必要条件 、必要非充分条件、充要条件、既非充分也非必要条件)? 并证明你的结论.
(1)f(x)是奇函数,(2)a ??2是![]() 的充分非必要条件
的充分非必要条件
解析:
A={x|![]()
![]() ∴ -1<x<1
∴ -1<x<1
∴A=(-1,1),定义域关于原点对称
f(-x)=lg![]() = lg
= lg![]() =
=![]() lg
lg![]() , ∴f(x)是奇函数.
, ∴f(x)是奇函数.
(2)B={x|![]()
![]()
B=[-1-a,1-a]
当a ??2时, -1-a??-3, 1-a??-1,
由A=(-1,1), B=[-1-a,1-a], 有![]()
反之,若![]() ,可取-a-1=2,则a=-3,a小于2. (注:反例不唯一)
,可取-a-1=2,则a=-3,a小于2. (注:反例不唯一)
所以,a ??2是![]() 的充分非必要条件。
的充分非必要条件。

练习册系列答案
相关题目
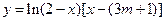 的定义域为集合A,集合 B={
的定义域为集合A,集合 B={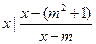 <0}.
<0}. 时,求A
时,求A B;
B;  A的实数
A的实数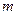 的取值范围。
的取值范围。 ,设函数
,设函数 的定义域为集合
的定义域为集合 ,集合
,集合 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 的定义域为集合A,函数
的定义域为集合A,函数
 和
和 。
。