题目内容
下列函数中,在其定义域内既是增函数又是奇函数的是( )
A、y=-
| ||
| B、y=x3+3x-3-x | ||
| C、y=log3x | ||
| D、y=3x |
分析:要探讨函数的奇偶性首先研究函数的定义域是否关于原点对称,由此排除C,根据图象排除A,D.即可得答案.
解答:解:对于A:∵y=-
在其定义域内不是单调函数,∴A不对.
B、f(-x)=-x3+3-x-3x=-f(x),∴f(x)为奇函数.又∵y=3x和y=x3和y=-3-x都是增函数,由函数的单调性知y=x3+3x-3-x增函数.B对;
∵C选项,函数的定义域为(0,+∞)不关于原点对称,∴C不对.
又∵D选项函数的图象既不关于原点对称又不关于y轴对称,∴y=3x不是奇函数.∴D不对.
故选B.
| 1 |
| x |
B、f(-x)=-x3+3-x-3x=-f(x),∴f(x)为奇函数.又∵y=3x和y=x3和y=-3-x都是增函数,由函数的单调性知y=x3+3x-3-x增函数.B对;
∵C选项,函数的定义域为(0,+∞)不关于原点对称,∴C不对.
又∵D选项函数的图象既不关于原点对称又不关于y轴对称,∴y=3x不是奇函数.∴D不对.
故选B.
点评:本题主要考查常见函数的奇偶性和单调性,以及判断函数奇偶性的方法,是基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
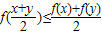 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数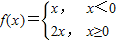
 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数