Question

（本小题满分12分）已知数列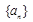满足，（）．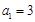

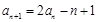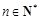（Ⅰ） 证明数列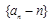是等比数列，并求出数列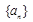的通项公式；

（Ⅱ）设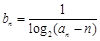，数列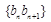的前n项和为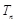，若对于任意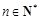，都满足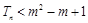成立，求实数m的取值范围．

 

Answer 1

【答案】

（1）见解析；（2）或．

 

【解析】本试题主要是考查了递推关系式的运用，求数列的通项公式，以及求解数列的和，不等式的恒成立问题的综合运用。‘

（1）由于，（）．

那么构造等比数列的思想，得到，从而求解得到

（2）中由于由（Ⅰ）知，则

然后分析，利用裂项求和的思想得到前n项和，并证明结论。

（Ⅰ）证法一：由可得，又，则，

∴数列是以为首项，且公比为2的等比数列，

则，∴.

证法二：，又，则，

∴数列是以为首项，且公比为2的等比数列，

则，∴.

（Ⅱ）解：由（Ⅰ）知，则，则，

∴，

则

故,只需，解得或．