题目内容
数列{an}的前n项和为Sn,已知 ,n=1,2,…写出Sn与Sn-1的递推关系式(n≥2),并求Sn关于n的表达式.
,n=1,2,…写出Sn与Sn-1的递推关系式(n≥2),并求Sn关于n的表达式.
解:由Sn=n2an-n(n-1)(n≥2),
得:Sn=n2(Sn-Sn-1)-n(n-1),即(n2-1)Sn-n2Sn-1=n(n-1),
所以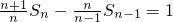 ,对n≥2成立.
,对n≥2成立.
由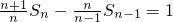 ,
, ,
, ,
,
相加得: ,又
,又 ,
,
所以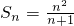 ,
,
当n=1时,也成立.
分析:由题设条件得(n2-1)Sn-n2Sn-1=n(n-1),所以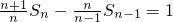 ,由此可以推导出
,由此可以推导出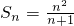 .
.
点评:本题考查数列的综合应用,解题时要注意公式的灵活应用.
得:Sn=n2(Sn-Sn-1)-n(n-1),即(n2-1)Sn-n2Sn-1=n(n-1),
所以
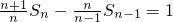 ,对n≥2成立.
,对n≥2成立.由
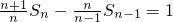 ,
, ,
, ,
,相加得:
 ,又
,又 ,
,所以
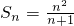 ,
,当n=1时,也成立.
分析:由题设条件得(n2-1)Sn-n2Sn-1=n(n-1),所以
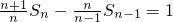 ,由此可以推导出
,由此可以推导出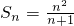 .
.点评:本题考查数列的综合应用,解题时要注意公式的灵活应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目