题目内容
已知抛物线P的方程是x2=4y,过直线l:y=-1上任意一点A作抛物线的切线,设切点分别为B、C.(1)证明:△ABC是直角三角形;
(2)证明:直线BC过定点,并求出定点坐标.
【答案】分析:(1)设A(m,-1),B(x1,y1),C(x2,y2),利用导数的几何意义可得  =
= x1,化简得
x1,化简得 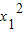 -2mx1-4=0.同理可得
-2mx1-4=0.同理可得 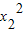 -2mx2-4=0,故有 x1+x2=2m,x1•x2=-4.计算AB和AC的斜率之积等于-1,从而得到AB⊥AC,即△ABC是直角三角形.
-2mx2-4=0,故有 x1+x2=2m,x1•x2=-4.计算AB和AC的斜率之积等于-1,从而得到AB⊥AC,即△ABC是直角三角形.
(2)求得BC所在的直线方程为 y-y1=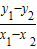 (x-x1),化简为y=
(x-x1),化简为y= mx+1,显然过定点(0,1).
mx+1,显然过定点(0,1).
解答:解:(1)证明:设A(m,-1),B(x1,y1),C(x2,y2).
∵抛物线P的方程是x2=4y,∴y′=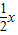 .
.
∴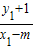 =
= x1,∴
x1,∴
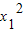 +1=
+1=
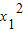 -
- mx1,∴
mx1,∴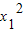 -2mx1-4=0.
-2mx1-4=0.
同理可得,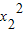 -2mx2-4=0,∴x1+x2=2m,x1•x2=-4.
-2mx2-4=0,∴x1+x2=2m,x1•x2=-4.
∵KAB•KAC= x1•
x1• x2=
x2=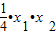 =-1,
=-1,
∴AB⊥AC,即△ABC是直角三角形.
(2)证明:BC所在的直线方程为 y-y1=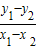 (x-x1),
(x-x1),
化简可得 y-
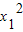 =
= (x1+x2)(x1-x2),即 y=
(x1+x2)(x1-x2),即 y= mx+1,
mx+1,
显然,当x=0时,y=1,故直线BC过定点(0,1).
点评:本题主要考查函数的导数的几何意义,判断两条直线垂直的方法,直线过定点问题,属于中档题.
 =
= x1,化简得
x1,化简得 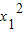 -2mx1-4=0.同理可得
-2mx1-4=0.同理可得 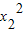 -2mx2-4=0,故有 x1+x2=2m,x1•x2=-4.计算AB和AC的斜率之积等于-1,从而得到AB⊥AC,即△ABC是直角三角形.
-2mx2-4=0,故有 x1+x2=2m,x1•x2=-4.计算AB和AC的斜率之积等于-1,从而得到AB⊥AC,即△ABC是直角三角形.(2)求得BC所在的直线方程为 y-y1=
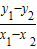 (x-x1),化简为y=
(x-x1),化简为y= mx+1,显然过定点(0,1).
mx+1,显然过定点(0,1).解答:解:(1)证明:设A(m,-1),B(x1,y1),C(x2,y2).
∵抛物线P的方程是x2=4y,∴y′=
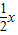 .
.∴
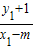 =
= x1,∴
x1,∴
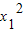 +1=
+1=
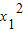 -
- mx1,∴
mx1,∴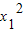 -2mx1-4=0.
-2mx1-4=0.同理可得,
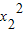 -2mx2-4=0,∴x1+x2=2m,x1•x2=-4.
-2mx2-4=0,∴x1+x2=2m,x1•x2=-4.∵KAB•KAC=
 x1•
x1• x2=
x2=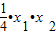 =-1,
=-1,∴AB⊥AC,即△ABC是直角三角形.
(2)证明:BC所在的直线方程为 y-y1=
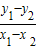 (x-x1),
(x-x1),化简可得 y-

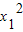 =
= (x1+x2)(x1-x2),即 y=
(x1+x2)(x1-x2),即 y= mx+1,
mx+1,显然,当x=0时,y=1,故直线BC过定点(0,1).
点评:本题主要考查函数的导数的几何意义,判断两条直线垂直的方法,直线过定点问题,属于中档题.

练习册系列答案
相关题目