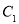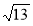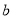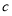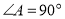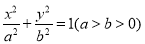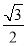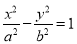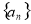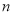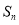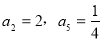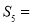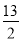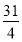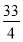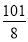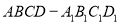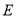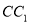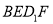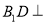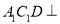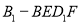题目内容
已知数列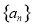 的前n项和
的前n项和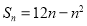
(1)求数列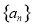 的通项公式,并证明
的通项公式,并证明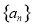 是等差数列;
是等差数列;
(2)若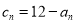 ,求数列
,求数列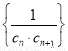 的前
的前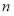 项和
项和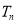
(1) 通项公式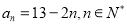 ,证明过程详见试题解析;(2)
,证明过程详见试题解析;(2)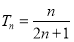 .
.
【解析】
试题分析:(1) 先根据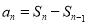 ,求出当
,求出当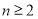 时
时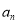 的表达式;再验证
的表达式;再验证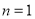 时是否满足;证明
时是否满足;证明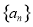 是等差数列,即证明
是等差数列,即证明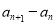 是定值即可;(2)先求出
是定值即可;(2)先求出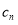 的表达式,再用裂项相消法求数列前n项和.
的表达式,再用裂项相消法求数列前n项和.
试题解析:(1)当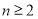 时,
时,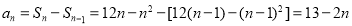 3分
3分
当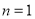 时,
时,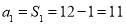 适合上式,所以
适合上式,所以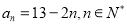 4分
4分
因为当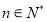 时,
时,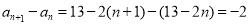 为定值,
为定值,
所以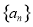 是等差数列 6分
是等差数列 6分
(2)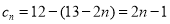 ,
,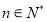
所以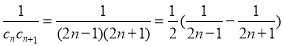
所以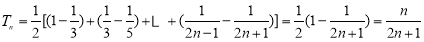 12分
12分
考点:数列通项公式的求和、数列求和.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
在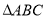 中,
中,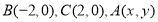 ,给出
,给出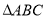 满足的条件,就能得到动点
满足的条件,就能得到动点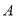 的轨迹方程,下表给出了一些条件及方程:
的轨迹方程,下表给出了一些条件及方程:
条件 | 方程 |
① |
|
② |
|
③ |
|
则满足条件①、②、③的点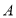 轨迹方程按顺序分别是
轨迹方程按顺序分别是
A. 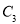 、
、 、
、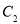 B.
B. 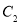 、
、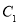 、
、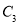
C. 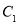 、
、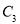 、
、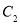 D.
D. 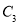 、
、 、
、